溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)を拝読中。今回は48ページ「3.4 級数解」の中の「3.4.1 線形微分方程式」です。前回につづき数学素人老人には恐ろしい無限級数登場デス。分かってる人にはこの形なら級数解ね、と瞬時に分かるみたいですが。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
※「例によって」Googleの生成AI、Gemini 2.5 Flash 様に解法をご指導いただいております。
今回の例題
演習ノートの「3.4 級数解」の中の「3.4.1 線形微分方程式」には例題がいくつかあるのですが、今回は以下の微分方程式を解く「例3」に取り組みたいと思います。取り組むといって例によってGoogleの生成AI、Gemini 2.5 Flash様に丸投げだったりしますが。
2* x^2 * y” – x * y’ + (1 – x^2) * y =0
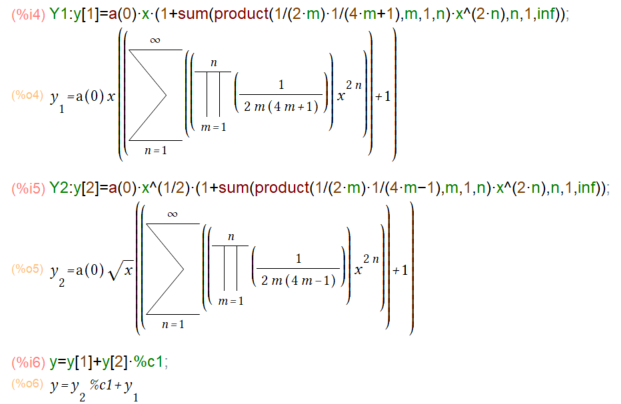
今回は先に、上記の解を掲げておきます。こんな感じよ。
\( y_1 = a(0) x ((\sum\limits_{n=1}^\infty (\prod\limits_{m=1}^{n} \frac{1}{2m(4m+1)})x^{2n})+1) \)
\( y_2 = a(0) \sqrt{x} ((\sum\limits_{n=1}^\infty (\prod\limits_{m=1}^{n} \frac{1}{2m(4m-1)})x^{2n})+1) \)
\( y = C\,y_2 +y_1 \)
解が無限級数の和になるというこってすか?
一応例題の微分方程式を ode2 関数に渡してみたところが以下に。緑枠が入力の微分方程式です。
つれなく false とな。なお、例1、例2は ode2関数で解けてしまい、イマイチ級数展開する御利益が感じられません。上記のようにode2でそのまま解けない例3が解ければ霊験あらたか?
Googleの生成AI、Gemini 2.5 Flash 様に投げかけてみる
今回はGemini様に先にお願いしてみました。その出だしが以下に。
おお、微分方程式を与えただけなのに、Gemini様は既に「級数解」を試す方針だそうです。Frobenius法とな。これも後でお教えいただきます。
上記の後、「なんだかんだ」で約3ページのご説明が続きますが、淡々とした記述が続くので割愛させていただきました。クライマックス付近が以下に。
上記の赤枠内が解ということであります。ここで 「…」 をつかった表現ですが、無限級数が出てきておりますな。一番最初に掲げた「解」の式と上記の赤枠内の「展開された」形が同じものに見えてきました?同じっすよ。
なおこの後、Gemini様はもしかして前回登場のベッセル関数などつかえるじゃないかとちょっと考えていらっしゃいましたが、それはムズイということで上記が最終回答デス。
フロベニウス法
Gemini様から「フロベニウス法」というご指摘あったので、ついでに教えてもらってます。
そして、上記の微分方程式例に対して Frobenius法を適用したときの解釈についてまで、ご説明いただけとります。こんな感じ。
こんだけお教えいただいてしまうと、何も言うことはねえ~。今回はGemini様に丸投げで良いです。いいのか?
演習ノートの解法、勿論Maxima使用
一応、以下にMaxima使った場合のクライマックスシーンを掲げておきますが、実はそれ以前の長い長いステップは何も実施してないです。演習ノートに解法掲げられておりますが、冒頭のkill除いて94ステップもあります。まあ演習ノートによると級数解による解法は手順がほぼほぼ以下同文なので、ひとつやっておけばチョイ変で対応可能らしいです。でも大変だよ。無限が94ステップで求まるんだから文句言うんじゃねえ。
中身は同じものの(筈だけれど)、大分、雰囲気は違う。なんだそれ。