前の3回はヒルベルト変換フィルタを使った周波数シフタだったですが、今回から、Weaver変調器による周波数シフタです。Weaverって何(誰?)と問えば、高名な(当然知らないとモグリ的な)発明者の御名前であったです。原理をなぞるのに三角関数の計算が必要。霧のかかった頭をMaxima様がお救いくださります。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※以下は、勝手に手習ひさせていただいております教科書へのリンクです。
三上直樹先生著、工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
上記教科書の6.4「Weaver変換器」による「位相シフタ」が手習ひのターゲットであります。
Weaver(ウエーバー)構造
上の三上先生の教科書ではWeaver変調器の説明は表裏2ページ弱で直ぐにArm Mbed上でのプログラムの実装に入っていってしまいます。Weaver先生を「誰?」とか言っている私としては、も少し説明が欲しいところ。そうしたら以下のページを見つけました。著者は、アナログデバイセズの石井聡先生です。石井先生がアナデバ様に移られる前の無線の会社にお勤めの頃、当時私が勤務していた田舎の会社までわざわざお越しいただいてお話をうかがったことがあるのです。爪の垢を煎じて飲め、と言われそうな偉大なエンジニア様です。
TNJ-033「ejωt」を考えるなかで出会うイメージ除去ミキサや超高速ADC(中編:イメージ除去ミキサなるものを考える)
なお、上記では、ハートレー構造とウエーバー構造を並べて図解されていますが、詳しく説明されているのはハートレー構造の方です。
三角関数の計算
今回の処理の原理は、高校で三角関数(加法定理とかいろいろ)を勉強していたら多分即座に分かりそうです。私は石井先生著の電気数学の教科書「持って」ますが、まったく身についておりませぬ。そこでお願いすることになりますのが、定番数式処理ソフトウエア、Maximaです。フリーですぞなもし。最近、以下の別シリーズにてMaximaを使っているので、多少「慣れた」感じがしないでもないです。ホントか?自分。
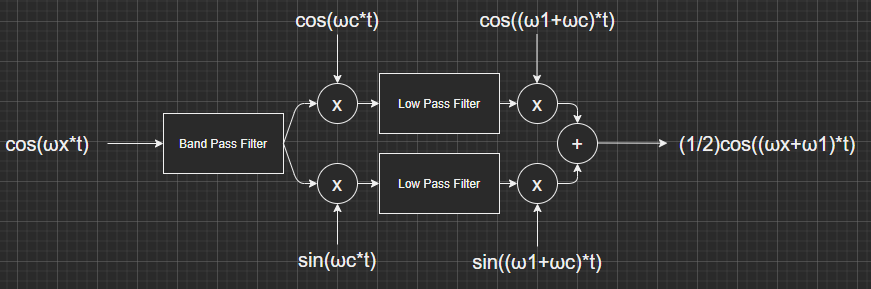
冒頭のアイキャッチ画像に処理の流れを示しましたので、流れにそってMaximaで式変形をしていきたいと思います。
以下でω(角周波数)関係のシンボルが複数でてまいりますが以下の意味です。
-
- ωx 元の入力信号の角周波数
- ω1 シフトさせる角周波数。出力はωx+ω1にしたい。
- ωc 入力信号の大域の中央の角周波数
ブロックダイアグラムでは、最初にバンドパスフィルタがありますが、これは周波数シフト後にナイキスト周波数を超えてしまうような周波数の信号を予め除去するためのフィルタだそうです。実処理では、サンプリング周波数10kHzで計算しています。
以下では、入力信号に insig と名前をつけて cos側の計算を追ってみています。
-
- interA 入力信号にωcのCOS波を乗じる
- interA2 上記の信号を和の形に変形
- interA3 和の形を項で分離しやすくする
- LPFinterA3 上記の2項のうち、LPF通過する周波数が低い項のみとりだす
上記で、LPF通過後のCOS波が得られると。
上記で、LPF通過後のSIN波も得られました。
続いて、COS波には cos((ω1+ωc)*t)、SIN波には sin((ω1+ωc)*t)を乗じたのち、加え合わせてみます。するとあれれ不思議ね、邪魔なωcが消えてなくなり、シフトアップ?されたCOS波が残ります。
こうしてステップ毎に結果を眺めてみれば、当たり前っちゃ当たり前。でも最初からこの結果だけを見たらば、黒魔術かと。大丈夫か、自分。