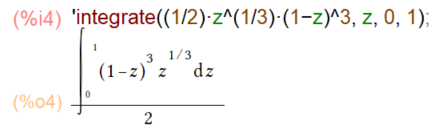今回も絶対に自力じゃ解ける気がしない定積分の例題です。ベータ関数に帰着するもの。だいたいベータ関数ってどんなんだっけ?「親類」にはガンマ関数とかヤバそうな奴らがいたような。しかし、Maxima様におかれましては一撃で解いておしまいになります。Maximaはベータ関数そのものも持っているのでそちらでもやってみるか?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
ベータ関数
Maxima自体は、beta(p, q)という形でベータ関数を求めることができます。ベータ関数についてのマニュアル(日本語)は以下に。
しかし、ベータ関数B(p,q)自体の形も朧気どころか、頭の片隅にもありませぬ。定義はこんな感じ。なお、p>0, q>0 です。
「分かりやすい」ベータ関数の解説ページを探していて、以下にあたりました。
拝見するに、大学受験対策用のページみたいっす。いや~今時の高校生のレベル高いです。自分が勉強してなかっただけか。
ベータ関数に帰着させる定積分の例題
定積分の例題とその解が以下に。自力じゃ解ける気がしない、それにベータ関数に帰着するとか思いつかない例題ですが、Maxima様にお願いすれば一撃と。
だいたいベータ関数に帰着させるというところまでに2手を要するのです。
-
- cos(x) = t とおいて置換積分
- t2=zとおいて置換積分
ようやくこの段階でベータ関数になるのかい?と見えてきます。後はp, q を求めてMaximaのbeta()で解いてみます。こんな感じ(p, q までsolveしておるとは、計算力の低下も極めりとな。)
お答えでました(解いたのはMaxima様だけど。)