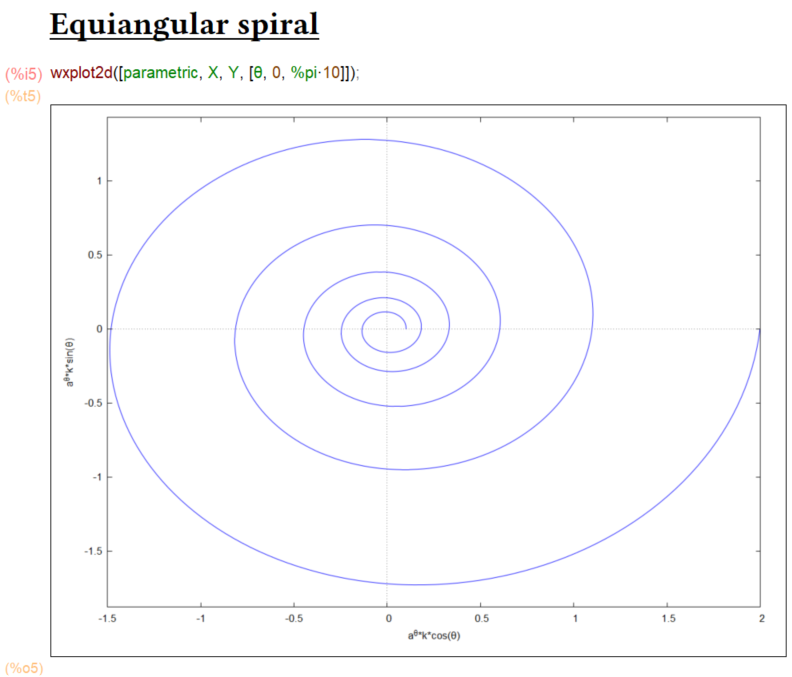
前回に引き続き「曲線の長さ(弧長)」を求めます。今回は極座標表示されている関数 r = f(Θ)、rは原点からの距離、Θは角度、のような形について練習します。例題はEquiangular spiral、等角螺旋、等角渦線、対数螺旋、ベルヌーイの螺旋などとも呼ばれる図形らしいです。ぐるぐるまき?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
Equiangular spiral
今回の問題の関数は r = k*a^Θ、rとΘを使った極座標で描ける図形です。ただし、k>0、a>0で、a≠1であります。
まずは図形を味わうためにプロットしてみます。パラメータプロットするのに極座標表示を直交座標に直してプロットしてます。なにかa、kに具体的な数字を与えないとプロットできないので、以下のような数字にしてみました。「緩くまく」か「きつくまく」かを決定しているのがaで、大きさをきめているのがkみたいです。知らんけど。
X: k*a^θ*cos(θ) Y: k*a^θ*sin(θ) a: 1.1 k: 0.1 wxplot2d([parametric, X, Y, [θ, 0, %pi*10]])
Maxima様に問題をお願いしているところが以下に。
極座標表示のときの弧長
弧長を求める「公式」は前回の延長?です。以下のようにとっても分かりやすい?ホントか?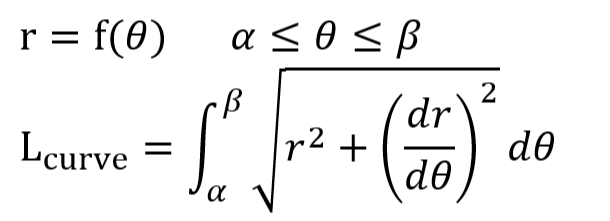
実際の問題は以下です。定積分するときはプロットと違って具体数値を与えなくても解けるので a, kのままですが、途中で正負とかいちいち聞かれるのがメンドイのでassumeのみしてます。
r: k*a^θ; assume(a>0, k>0); assume(notequal(a, 1));
Maxima様にお願いしたところが以下に。
後は、公式に当てはめて弧長を求めるのみ。
L: 'integrate(sqrt(r^2+diff(r, θ)^2),θ,α,β); ev(L, nouns); ratsimp(%);
今回は、ratsimp()一発で、宿題に提出できる程度の形になってくれたのでラッキー?