まだ偏微分の練習をしていて本題の微分方程式に行き着けませぬ。何時になるのか?といって手を抜いて進捗を速めるのみ?さて今回は2変数関数のマクローリン展開です。マクローリン展開はテイラー展開の特殊型?なのでtaylor()関数一発で求められます。しかし「マクローリン」というのを避けている気がするんだが、気のせい?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
taylor関数
普通の微分でも、偏微分でも全微分でも、1階だろうが2階だろうが微分はdiff()関数ひとつに全部お任せでした。同様に、テイラー展開だろうと、マクローリン展開だろうと、1変数だろうと多変数だろうと、2次の項だろうともっと先までだろうとtaylor()関数に全部お任せです。いつもお世話になっておりますMaximaの日本語ドキュメントの関係ページが以下に。
28. Sums, Products, and Series
ただ、taylor()関数の説明をみると分かるとおり、引数の取り方、やたら多いです。やってみると引数の与え方で処理の順番も変わるような。知らんけど。
練習問題その1
多変数関数のマクローリン展開の場合、上のように第2引数に変数リスト、第3引数にマクローリン展開なので[0,0]とし、第4引数に各変数の打ち切り次数のリストを与えるという方法が良いのではないかと思います。
なお、結果のところ、(%o2)/T/ のように/T/とあるのは、第53回で登場した標準有理式(CRE)のテイラー級数用拡張形態らしいっす。「無限に続く」項を表現できる形態とな。
練習問題その2
つづく練習問題も淡々と解けるかと思いきや1点お間抜けで躓きました。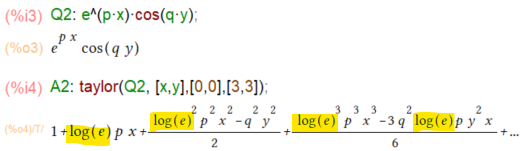
黄色くマーカを引いた部分です。ここでlog()関数は自然対数なので、log(e)は1じゃねえの?なんで1にしてくれないの。
log(e)を1に評価してもらおうと頑張りましたが無理。そこでようやく気付きましたです。Maxima上で自然対数の底、ネイピア数は、%eと書くのではなかったっけ?上のlog(e)というのは%が抜けております。元のQ2式をみたらばあちゃ~、悪いのは自分。訂正させていただきます。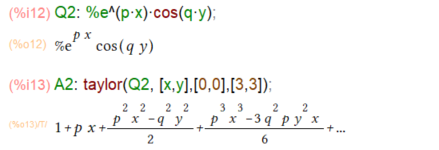
よかったちゃんと解けた。ついつい 素のe とか書いちゃう忘却力。