前回で長きにわたった「多変数関数の微分」を終えられた（ホントか？）ので、今回から「多変数関数の積分」デス。一難去ってまた一難という感じか？実際に計算しているのはMaxima先生なので私は何も苦労はないのですが。今回は積分領域Dが長方形で定数で決まる繰り返し積分。重積分へいたる中では一番お楽な感じの奴らか。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
例題１
例題１はとてもシンプルです。こんな感じ。
教科書的には以下を頭に入れて計算せよ、という思し召しみたいです。そうすりゃ計算簡単になりそうだし。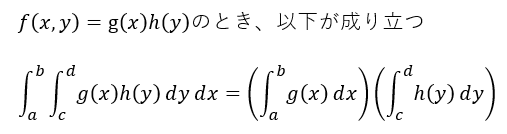
しかし、当方Maxima先生にお願いするので、そのままの形で入力してみます。
Ex1: 'integrate('integrate(x^2*y, y, 0, 2), x, 0, 3)
「そのままの形」で入力が、Maxima先生の内部では教科書の思し召しどおりに掛け算の形に変形されてました。
答え一発１８とな。
例題２
例題２は、g(x)*h(y)みたいな形では書けない関数なのでそのままの形で入力。
x2: 'integrate('integrate((x-y),x,1,2),y,1,3)
有無を言わさずお答えは求まりますです。こんな感じ。
例題３
例題３は、積分領域の上限が文字定数になってます。そんなこともお構いなし。
ただ、教科書的には因数分解された形がご所望ということで、最後 factor()関数にお出ましを願って解決。
今回はただただ問題通りに入力すればほぼ一撃でお答えに至る。お楽でよかった。