前回、「積分範囲にマルでも三角でももってこい」と書いたらば、今回はホントにマル(半円ですが)と三角でした。ということで今回は前回の続きみたいな感じです。だだし教科書には『まず領域Dを図示して』とご指示ありです。この領域Dの図示が出来てしまえば入力は簡単。後はMaxima様に計算お願いするだけ。いつものとおりの一撃。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
例題1
まず例題の式の入力にはMaxima様ではなく、別なソフトで清書といたしました。Maxima様だといくらシングルクウォートで評価を抑えても処理されてしまう部分があるので。また、不等号を並べるような不埒な?書き方は許されないようでもあります。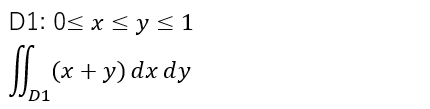
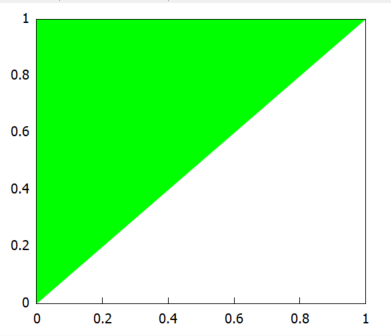
今回は、領域を図示せよ、とご指示にあります。まずは上記のD1の領域をグラフ化するところから。Maxima様にD1を塗りつぶしてもらうためのコマンドが以下に。
draw2d(fill_color=green, filled_func=1, explicit(x, x, 0, 1));
実際のプロットが以下に。三角でやんす。
上のようにD1が明らかになったので、二重積分として入力してみます。いつものとおりシングルクウォートで積分記号のまま評価を一度おしとどめた後、改めて評価する方法です。
Maxima様にお願いすればお答えは一撃。
例題2
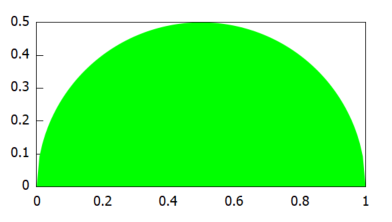
こちらの領域D2はちょいとムツカシーです。といって半円ですが。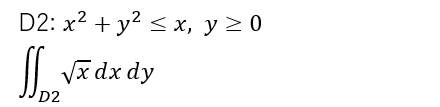
陰関数の形であるとメンドイので、solveを使って、y=の形に直しておきます。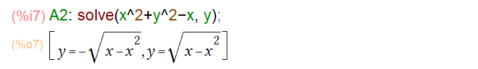
正と負の両方の解が得られましたが、y≧0なので、2つ目の方A2[2]が求めるものです。D2領域を塗りつぶすためのコマンドが以下に。
draw2d(fill_color=green, filled_func=rhs(A2[2]), proportional_axes = xy, explicit(0, x, 0, 1));
上記のようにD2が「分かった」ので、あとはMaxima様に積分をお願いするばかりです。yが含まれていない被積分関数なので、入力は2重積分ですが簡単にされてしまってます。
やはり答え一発。何もすることはありません。よかった。