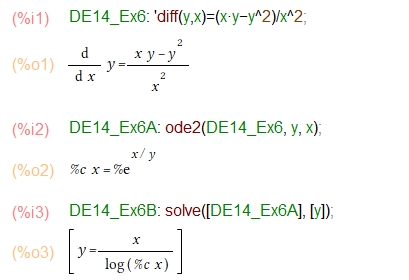前回はode2()関数で初期値問題。今回は一般解を求める問題に戻ります。「同次数微分方程式」とな。教科書は「簡単に変数分離形に変形できる」としてテクをお教えくださっているのです。しかしMaxima様のode2()関数にお願いすれば、そんなテクなど不要、一撃解答(後処理にひと手間いることもあるけど。)いいのかそんなことで。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
同次(同次形)微分方程式
教科書を引き写せば以下のとおり。この形の微分方程式であれば変数変換によって変数分離形に帰着できるのだ、と。
しかし、つべこべ言わずode2()にお願いすれば一撃です。
今回の例題3つ
教科書的にはまず右辺を変形してy/xの関数であることを確かめておいてから変数変換、そして変数分離形の公式に当てはめて微分方程式の解を求めています。こちらでは最初からode2()関数にお願いしてます。メンドイことは皆Maxima様まかせ。
上記の%o2のようにyが身もふたもない所にいらっしゃるので、やはりy=の形がええ、ということでsolve()関数で後処理してます。ちょっと1撃ではなかったな。最初から。
2番目の例題っす。これは一撃。何も考えなくてもお答えがでるっと。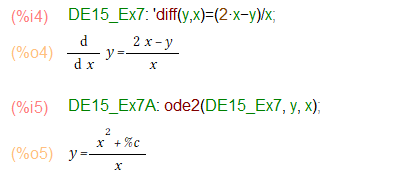
3番目の例題。これは教科書もこの形(…=%c)でOKとしてらっしゃったので、あえて後処理はしてません。メンドそうだし。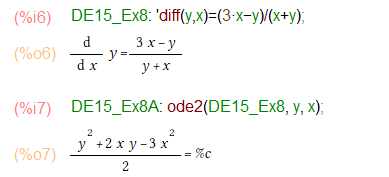
いいのかこれで。ode2()に頼っていると確実にお馬鹿になるな、いや頼る前からそうか?