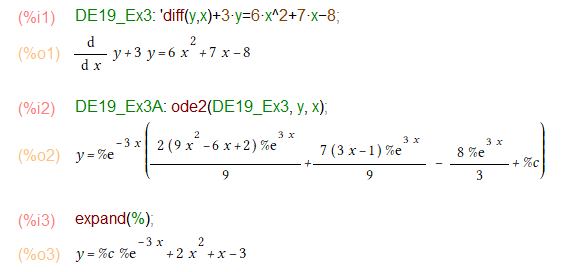前回は定数係数一階微分方程式、前々回は同次微分方程式でした。今回はそれらを踏まえて?教科書では「未定係数法」だったです。武道の形のごとく微分方程式も形の練習が大事だと。ホントか?しかし例によってMaxima様のode2関数におすがりすれば、未定係数法の例題だろうと何だろうと一撃、皆救われると。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
未定係数法
数学素人の忘却力の年寄が、教科書のこの部分に書かれていたことを「ホンワカ」まとめると以下のように思われました。違っとるかも知れんで。
ということで、教科書では特殊解の形を示し解き方をお教えいただいておるのです。ありがたや。しかし、ode2()関数に御すがりする場合は、そのままぶち込むだけの乱暴さ。
ode2()の出力のままだと、教科書的にはマズかろうということで、最後にexpandかけて展開すれば上記のように一般解が求まります。何も考えていね~。
三角関数の場合、DE19_Ex4Bの形でもOKだと思うのですが、教科書のお答えとしては5/6を乗じてやって係数をシンプルな形にした方がよろしいようで。rhs()のみ取り出して整理したものが上記に。上の黄色のマーカー部分を改めて%Cとおきなおすとバッチリなのですが。。。
これは最後にexpand()すれば所望の形にハマりました。
裏側は知らず、ぜんぜん未定係数法らしい計算見えないじゃん。