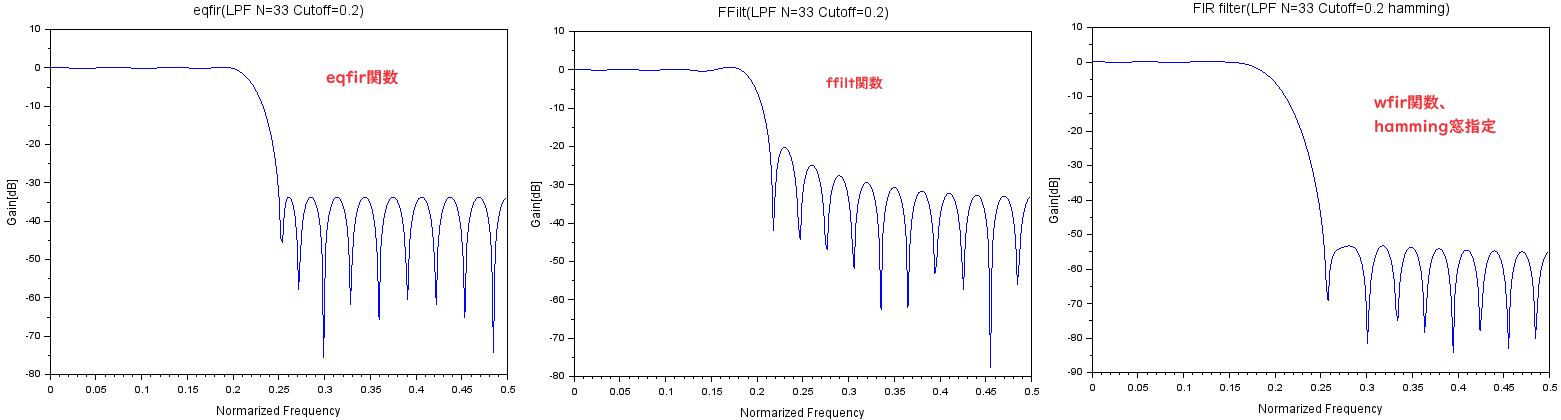
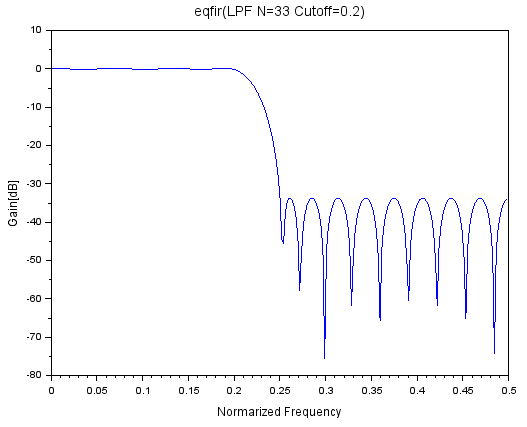
過去3回、ScilabのFIRフィルタ設計関数3種について同条件(33次、ローパス、正規化カットオフ周波数0.2Hz)でフィルタ係数を求めてきました。今回は第4の設計関数 eqfir を使用してみます。eqfirは「ミニマックス近似」ということなので、インパルス応答を近似した多項式の一番良さげなやつで求めたってこと?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1(以下comm_tbx)を使用させていただいとります。
第4の設計関数 eqfir
過去回を振り返って設計関数を列挙すると以下のようです。
-
- fsfirlin、周波数標本法
- wfir、ウインドウィング法
- ffilt、不明な算法?
- eqfir、ミニマックス近似
今回はその末尾、eqfir関数を使用してみたいと思います。「ミニマックス近似」ということなので、無限なインパルス応答を有限な点数の多項式で近似したものの「一番いいやつ」ということなのでしょう。知らんけど。
さて、いままでのどの関数も引数はクセ強で、それぞれ我が道を行ってました。今回のeqfir関数も同様です。eqfir関数のhelpページが以下に
上記ページには各引数の説明が書かれてますが、そっけないです。
第1の引数nfについては、次数(フィルタ係数の点数)ということでよさそうだね。
第2の引数bedgeについては『Mx2行列で, 各バンドの境界の組を指定』と書かれてます。Mってなんだ?何も書かれてないようです。素人老人は戸惑うのですが、上記ページの例などみると、通過域、阻止域毎にその始まりと終わりを並べていくのでx2であるようです。今回ローパスフィルタで、正規化周波数0.2Hzまで通過、そのあとに阻止域がくるので、以下のようにしてみました。
[0 .2; .25 .5]
.2から.25の間は定義してないので遷移帯のつもり。なお、正規化周波数なので末尾の.5はナイキスト周波数デス。
第3の引数desについても『M次ベクトルで,各バンドで指定する振幅を指定』などと書かれていてサッパリです。でもま、通過域はゲイン1,阻止域はゲイン0と考えて以下のようにしてみました。
[1 0]
第4の引数wateについては『M次ベクトルで,各バンドの誤差の相対重みを指定』です。「相対重み」ってなんだ?素人老人にはよくわからないものなので、とりあえず「相対重み」で何かしたりしないというつもりで以下のようにしてみました。
[1 1]
フィルタを生成してその周波数応答を調べる
過去回で何度も同じことをしているので大分なれました。フィルタを作ってその周波数応答を調べるコードはこんな感じ。
x=eqfir(33, [0 .2; .25 .5],[1 0],[1 1]);
[hm,fr]=frmag(x,256);
plot(fr,20*log10(hm));
xlabel("Normarized Frequency");
ylabel("Gain[dB]");
title("eqfir(LPF N=33 Cutoff=0.2)");
ローパスフィルタになっているみたい。あたりまえか。
引数の指定の仕方などほぼほぼ無限。わからんよなあ。。。