
LTspice配下のExampleフォルダ内Educationalフォルダ所蔵の回路図を巡回中。今回はMonteCarlo。乱数のお助けでなんだか高級なシミュレーションができるモンテカルロ法、素人老人は大好きですぞ(個人の感想デス。)LTspiceにおいては電子部品に必然の部品のばらつきを盛り込むことに意義を持つと。
※「SPICEの小瓶」投稿順インデックスはこちら
※アナログデバイセズ社のLTspiceのガイド、ヒント、便利な情報については以下へ。https://www.analog.com/jp/resources/design-tools-and-calculators/ltspice-simulator/ltspice-recommended-reading-list.html
お惚け老人など、普段、部品の公称の数値をもってシミュレーション一撃にて、出来た出来たなどと喜んでます。しかし、電子部品にはバラツキがあるのであります。1撃にて出来たなどと喜ぶ素人老人とは違い、プロは「遅い」組み合わせとか、「速い」組み合わせとかコーナー条件と温度など組み合わせて「ほんとうに量産しても大丈夫だよね」というあたりを確かめます。そういうことをしないと、いざ量産したら、ロット壊滅などという憂き目を見ますな。知らんけど。
さらに言えば、設計者が想定する最悪の「コーナー」は本当にそこなのか?という疑問もあり、また、ギリギリでヤバイ部品と、ゆるゆるで楽勝な部品もありと各バラツキの意味も異なります。
そんな際、神ならぬ人の代わりに「乱数」光臨。バラツキの影響を統計的に評価するのだと。まあ、テキトーに組み合わせて数繰り返すんだけれども。
LTspiceにおけるモンテカルロ法
LTspiceにおいて、ざっくりモンテカルロ法の実施は以下の2ステップによるみたいです。
バラツキのある部品のパラメータを以下の乱数を使った関数で表現する。その際使える関数は以下の通り。
-
- mc(x, y)、公称値 x から ±y の範囲の一様分布
- flat(x)、-xからxの範囲の一様分布
- gauss(x)、標準偏差 x の正規分布
そして .step文を使って、シミュレーションを繰り返す。ここでダミーパラメータが現れるが、繰り返しの制御に使われるだけみたい。こんな感じね。
.step param X 0 20 1
これだけのことで、「いろいろバラつかせた」シミュレーションができるっと。お楽。
MonteCarlo.asc
今回、Educationalフォルダから取り出したのは
MonteCarlo.asc
なるファイルです。中身はバンドパス特性をもった受動素子回路みたいです。これの各部品について5%の精度を想定し、その範囲でのモンテカルロ・シミュレーション(AC解析)を行うらしいです。回路が以下に。
シミュレーション結果
上記のシミュレーション後のAC解析のプロットが以下に。実線がゲイン、点線が位相っす。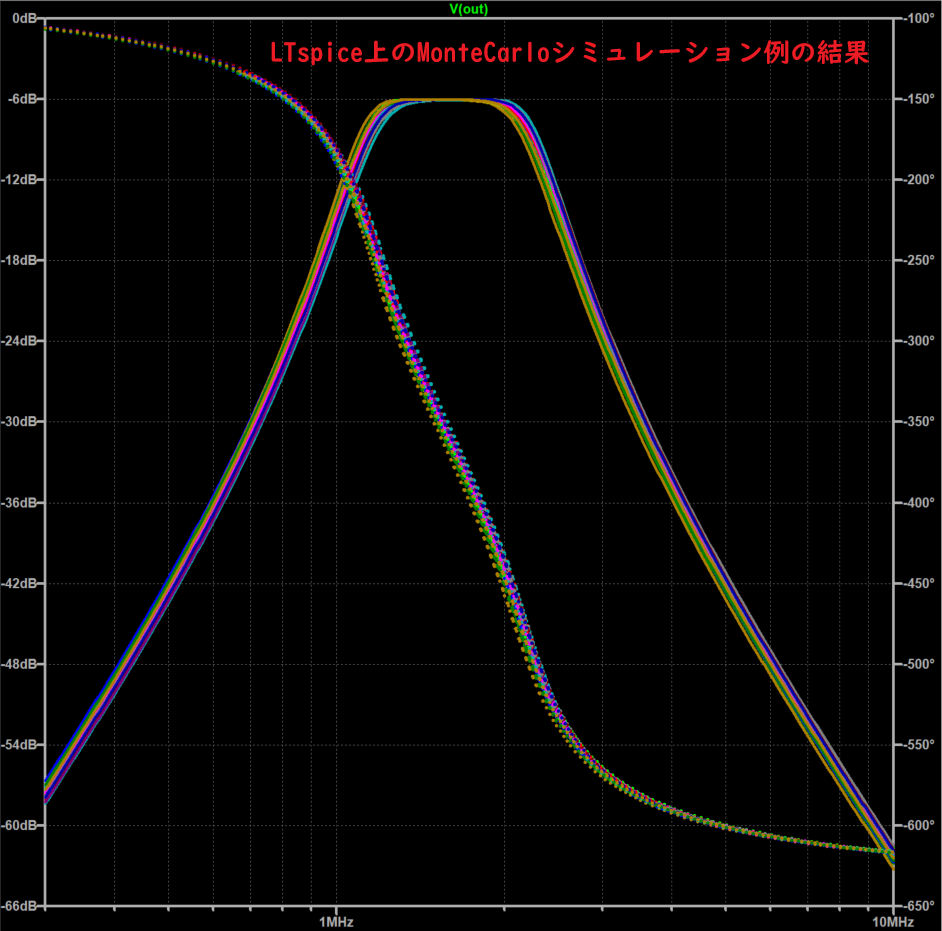
合計20回の異なるパラメータによるシミュレーション結果が重なっているので、グラフは幅を持ってます。
このくらいのバラツキを許容できんならば、お前の設計は失敗だと。おっとシミュレーションでよかった。