先週「アナログコンピュータ」ネタに手を出してしまい、ついつい微分方程式やらねば(思い出さねば)などと無駄なことを考えてしまいました。そこで「手頃な題材」として、コロナの感染モデルの方程式を解いてみるのはどうでしょうか。テレビじゃ方程式はでてこないけれど、良く出ているグラフを見ればきっと微分方程式に違いない。ネット探せば、方程式くらい直ぐに見つかるだろ、と考えました。
※「忘却の微分方程式」投稿順 index はこちら
※2025年8月14日追記:データからSIRモデルのパラメータを推定する件はこちら
「コロナ 微分方程式」で検索すれば、直ぐに見つかりました。私の場合、検索結果のトップはコロナ感染の流向予測に関する東大の先生のプレゼン資料(参考になりました)であったのですが、2番目、3番目は、
コロナ社の微分方程式関係の書籍などのページ
でした。コロナ違いであります。コロナ社、学生のときお世話になりました。しかし、コロナ繋がりで、コロナ社に変なトバッチリは飛んでないか、ちょっと心配になりました。余計なお世話ですが。結構いろいろヒットしてくる多くのページを読ませていただき、以下のように勝手に理解させていただきました。
-
- 一番簡単なモデルがSIRモデル
- その次に簡単なモデルがSEIRモデル
- 研究的にはもっと精緻なモデルがいろいろ提案されている
SはSusceptibleで未感染で感染する可能性のある人、IはInfectiousで発症した人、RはRecoveredで回復した人、ということのようです。2番目のモデルは、SIRに加えて、Exposed、潜伏期の感染者(感染力無)をさらに想定するもの。要はいずれのモデルもS,I,Rなどの人数の変化率(微分)はこう書ける、という式を立てて解いておるわけです。
今回本題は、微分方程式を思い出そうということだけなので、なにもコロナ感染の予測をしようなどとは微塵も考えておりませぬ。そこで、一番簡単なSIRモデルで計算してみることにいたしました。その際、参考になったのが、以下のカシオさんの計算サイトに会員のtonagaiさんが投稿されている
のページです。ご存知かもしれませんが、カシオさんの計算サイトは、電卓さながらに値を入力すればWeb上で結果が出てきます。なかなか面白いケースが沢山あるので、個人的には好きなサイトです。こういうページがあるとモデル作って動かした後の「検算」が楽。ぶっちゃけ、同じパラメータで動作させれば、まずまず同じ結果が得られる筈。なお、tonagaiさんはSEIRモデルも投稿されてますのでご興味のある方はSIRモデルのページから辿ってくださいまし。
さて、当方での「実装」ですが、以下のような方法を考えました。この辺は切っ掛けになったアナログコンピュータ・ネタと同じです。
-
- オペアンプとブレッドボードでハードウエア実装(アナログコンピュータもどき)
- LTspiceで上記回路を電子回路としてシミュレーション
- 微分方程式とけるソフトを利用させていただく
オペアンプで回路を作ってお手軽ツールで実験してみる、そのとき、アナデバ社のLTspiceでシミュレーションする、というのは別シリーズでやっているので、ここでは却下です。このシリーズでは、3の、微分方程式を解けるソフトを利用させていただく、という方針。そのとき、パッと頭に浮かんだソフトウエアは以下のようなものであります。
この中で、一番「使いたかった」のはMatlabのお供プログラムといっていいでしょうか、Simulinkというものです。ブロックダイアグラム的な図を描いて、時系列データに関してモデルを作り、それを(数値的に)解くことが簡単にできるものです。私は、誓ってMathworks社の回し者ではありませんが、
Matlab使えるなら、Matlab使うのが一番いい
という意見です。あの充実した(日本語)helpを読んでいるだけでも、なにか立派な人になったんじゃないか(錯覚ですが)という気分になります。しかし、何分、ライセンスがお高い。商用ライセンスは勿論、それより一桁安い社会人向けの非商用ライセンスでもとても手がでません(Matlabの場合、本体以外に別売のツールボックスなるものがいろいろ「欲しくなる」のです。そいつらを買っているとみるみるうちに金額が膨らみます)。ですから、さらにもう一桁安い学生用ライセンスで買える学生さんはとてもうらやましい。それどころか、
理工系大学では大抵無償のMatlabライセンス
が使える筈(大学のどこかにライセンスの窓口あるでしょ、きっと)。学生さんは、只で使えるうちにMatlabすべし、と思います(個人の見解です。)
Matlab互換的なツールとしては、ScilabとOctaveの2つが有名じゃないかと思います。私が使用したことがあるのは、どちらもかなり古いバージョンです。Matlabとの「言語の互換性」だけでいえば、Octaveの方が高かったような気がします。Scilabも互換性はあるのですが、「似ている」けれど、独自の世界を作り上げている、という感じ。Scilabの方には、Simulinkに相当するブロックダイアグラムで描いて解けるXcos(昔はScicosと言っていた。XMLベースになってからXcos言っている気がする)も含まれます。アナログコンピュータ風、で行きたい今回は、
ScilabのXcos使用
ということにいたしました。なお、他のプログラムも適宜使わせていただこうと考えております。なお、R言語については、まさに Rでコロナ 扱っているそのものズバリのページもありましたぜ。
さて、ようやく本題の
SIRモデル
に入ります。1階の連立微分方程式、という分類で良いですかね?だいたい「連立微分方程式」などと唱えるのは、大体何年、いや何十年ぶりかもしれない。
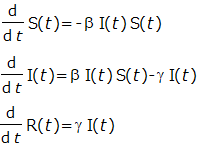 蛇足ですが、上の数式画像は、Maximaを使って記述して画像化しております。Maximaで書くとこんな感じ。
蛇足ですが、上の数式画像は、Maximaを使って記述して画像化しております。Maximaで書くとこんな感じ。
diff(S(t),t,1)=-%beta*S(t)*I(t); diff(I(t),t,1)=%beta*S(t)*I(t)-%gamma*I(t); diff(R(t),t,1)=%gamma*I(t);
さて、これをScilabのXcosでブロックダイアグラムで描くとこんな感じ。ことさらに
アナログコンピュータ風
にしてみたのですが、どうでしょうか。
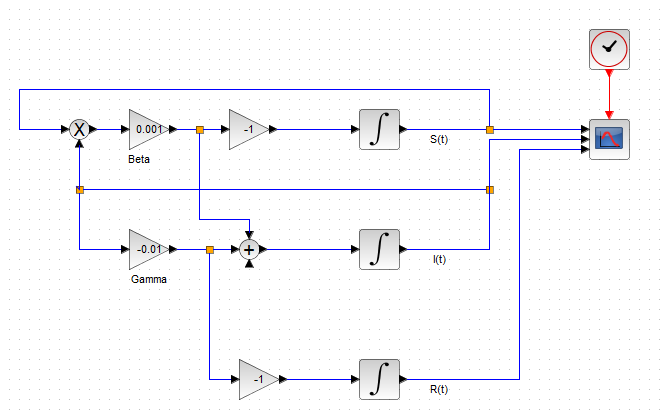 最初のグラフ、Beta, Gammaの設定値や、初期条件(積分器のt=0のときの値として設定する)は、上の tonagaiさんの設定 をそのままパクらせていただきました。ありがとうございます。
最初のグラフ、Beta, Gammaの設定値や、初期条件(積分器のt=0のときの値として設定する)は、上の tonagaiさんの設定 をそのままパクらせていただきました。ありがとうございます。
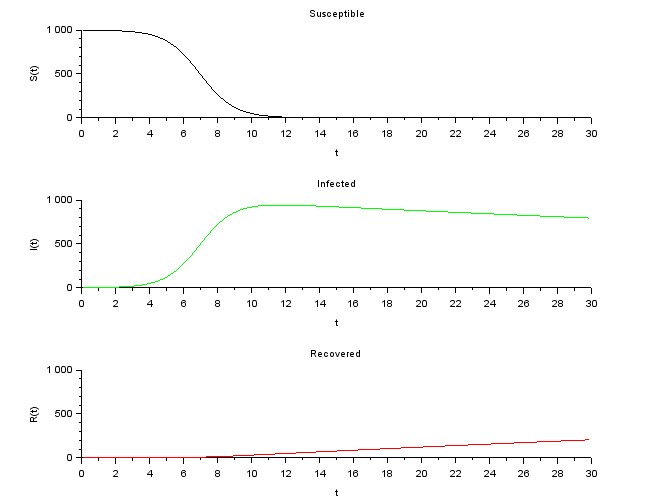
シミュレーションをRUNすると、こんな感じ(実際は、Scilabの使い方、ほとんど忘れていて、しばらく右往左往していましたが。)
 ぱっと見た感じ、tonagaiさんのSIRモデルのページのグラフと大体同じ?
ぱっと見た感じ、tonagaiさんのSIRモデルのページのグラフと大体同じ?
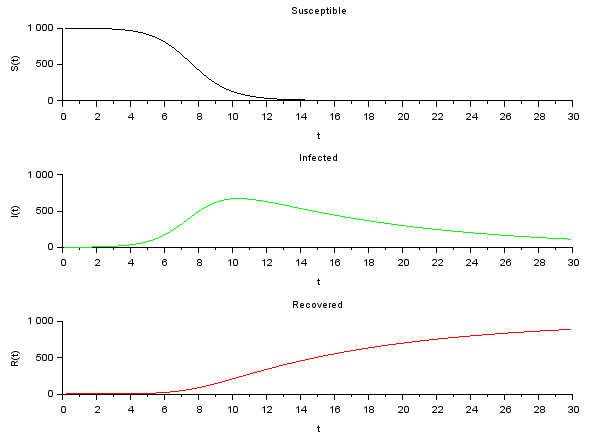
折角のシミュレーションなので、感染するレートを司るベータ値を10倍にしてみました。あっという間にまん延。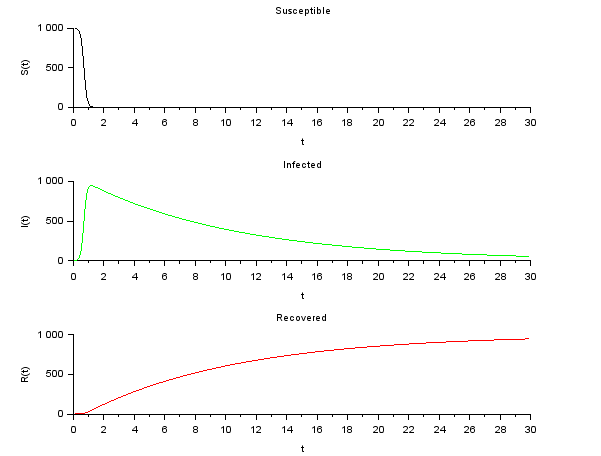
ベータを元に戻して、回復するレートを司るガンマ値を10倍にしてみると、恐ろしいことになかなか回復しなくなる。それどころか、よく考えるとこのモデルでは、死者数というのはモデルになく、結局、ガンマかけて「掃き出し」ている数字には、直った人も死んだ人も含まれている、と考えられます。もっと恐ろしい話であります。