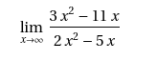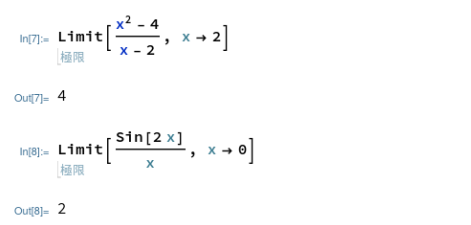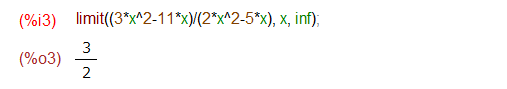今回は極限(limit)です。ようやく微分の入り口近くまでたどり着きましたな。でもま、先は長いです。流石にこの辺りは、MathematicaとMaximaどちらも「できる」感じです。入力から数学的で美麗なMathematica（その代りメンドイ）、と入力は素っ気ないMaximaという感じでしょうか。出力はどちらも美麗。
※「忘却の微分方程式」投稿順 index はこちら
あまり真面目にやっているわけでないのですが、進捗テーマは以下のWolfram社Mathematicaのチュートリアルを参照、準拠させていただいとります（学生でないのにすみません。）
今回は、Mathematica の入力書式の方が「読みやすい」という理由から、Mathematica 先攻で行きたいと思います。
極限の入力
Mathematicaでは、極限は Limit[] で求めることができます。以下は同じ極限値を求めたものですが、上の素っ気ない入力表現でも、下の分かり易い（そのかわりちょっと入力が面倒）な入力表現でも答えは求まります。
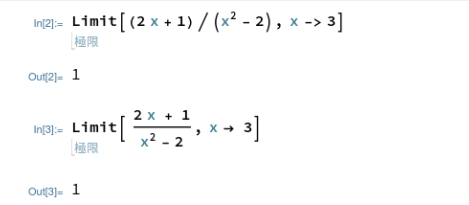Mathematica（Wolfram言語）の場合、入力時点で数学的なシンボルを使った表現が使えるので分かり易いです。入力方法については、以下に書かれているのを見つけました。
ノートブックへの入力 – Wolfram言語 & システム ドキュメントセンター
一方 Maxima（使用しているのはGUIを被せた wxMaximaですが）は、質実剛健、プログラム言語？的な素っ気ない入力です。
普通にお答えは求まるので、まあいいんですけれども、Mathematicaの入力表現を見てしまうと、パッと見、Mathmaticaの方が分かり易いな～と。。。
いろいろ極限を求めてみる。
分数式の極限と、そして高校のテストに確実に出そうな三角関数を含む式の極限が以下に。まずはMathematicaより。
同じことをMaximaでやってみたのが以下です。
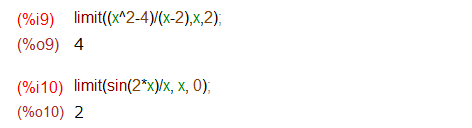
表現形式をのぞけば、このくらいのことは朝飯前か？（MathematicaもMaximaも朝飯食わんけど。）
今度は、お楽しみの無限大が出てくるやつ。Mathematicaの場合、∞のシンボルは、ESCキーを押した後 INF と書いてまたESCキーを押せばでてきます。
同じことをMaximaで入力したもの、無限大は素っ気なく、inf とな。
右極限、左極限
珍しく（？）、右極限、左極限の指定はMaximaの方が直観的に分かり易いです（個人の感想です。）
Mathematicaの場合、Directionで指定するのです。高校の教科書に必ず載っている筈の例 1/x では右極限が-1、左極限が1と指定です。行き先の方向を表している？
すみません、上のキャプチャの２番目の式のお答えが切れてました。勿論 -∞ であります。
MathematicaのDirection指定に対して、Maximaの場合、以下のように右極限は plus、左極限は minusと指定します。Maximaは出発する方を表している？頭の固い年寄りは右がプラス、左がマイナスと思い込んでいるので、こちらの方が感覚的に安心します（個人の感想です。）
Limitをそのまま表示する方法
Mathematicaの Limit[] も、Maximaの limit() も普通に入力すると評価されてしまいます。評価せずに「数学的な書式」のままで表示したいとき（レポートを書くときとかに使いたくなるのかな？）は、以下のようにできました。ここでも細かく制御できる（でもメンドイ）Mathematicaと、素早く入力できるMaximaという感じです。
まずはMathematicaです。出力表記を制御する関数が２つも存在します。
上と下の違いは微妙といえば微妙ですが、下の方が２つも関数重ねただけあってフォントも美麗です。
wxMaximaの場合、頭に ‘ (シングルクウォート）をつければ評価を抑止し、数学的な記法で残してくれます。
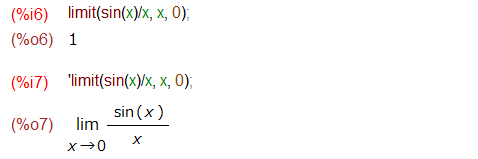多分、Maximaでもっと美麗な出力をさせたい場合は、きっとTEXとか出てくるであろうと思われる（勝手な想像です）のでこれ以上踏み込みませぬ。
極限やったから次は微分？