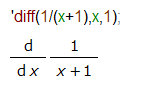前回が極限であったので、今回は導関数、微分であります。ようやくシリーズタイトルに近づきつつ（まだ先は長いけど）ある感じがします。通例、「分かり易い」Mathmaticaと「知っているべきことが多い」Maximaという感じ（個人の感想です）なのですが、今回は逆。Maximaの方がストレートな印象。ホントか？
※「忘却の微分方程式」投稿順 index はこちら
進捗テーマは以下のWolfram社Mathematicaのチュートリアルに「準拠」させていただいとります。
学生でもないのに参照させていただいていてどうもすみません。
導関数（微分）を求めるのと、ディーワイ・ディーエックス的表記
今回は、Maximaの方が分かり易く感じたので、Maxima先行で行きます。まずは、簡単な微分（とは言え、自分じゃ微分の公式などとっくに忘却の彼方）。
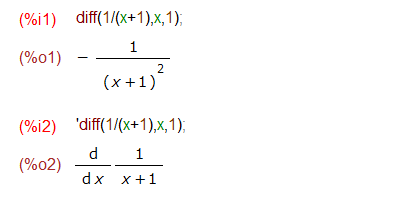Maximaの場合、微分を行ってくれるのは diff() 関数です。シングルクォートで、式の評価を止められるので、%i2のように頭にシングルクオートをつければ、ディーワイ・ディーエックス的な（何と呼ぶべきなのだろう？）表現のままで止めておけます。
一方、Mathematicaの場合、たった一文字の関数 D[] が微分です。Mathematicaは N[] とか一文字好きですな。
Mathematicaでも、ディーワイ・ディーエックス的な表現に留めたいとおもったので、HoldForm[]関数や、TraditionalForm[]関数を使ってみたのですが、上のように、偏微分（やっていることは間違ってないですけど）の表記になっています。どこかに表現を変える方法が書いてあるのか否や？でもま、内部でやっているとおりの表記なんでしょう。
さてMathematicaでは、シングルクォートを使っても微分可能です。数学の授業でおなじみのf ‘(x)の形。
ただ、下の例のように後から ‘ つけても微分してくれないみたいです。挙動がまだ分かりませんなあ。
当然、どちらも、N階の微分にも対応しとります。Maximaはこんな感じ。
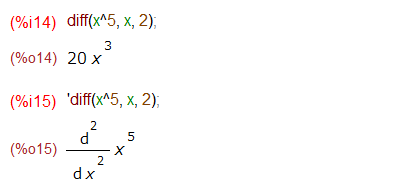Mathematicaの場合は、微分する変数名と微分の階数をリストにして与えるスタイルです。こんな感じ。
自分で定義した関数の微分
Maximaの場合、関数定義は := であることを知っていれば、以下のように普通のプログラミング言語風です。そして、それをdiff()関数に渡せば微分してくれます。
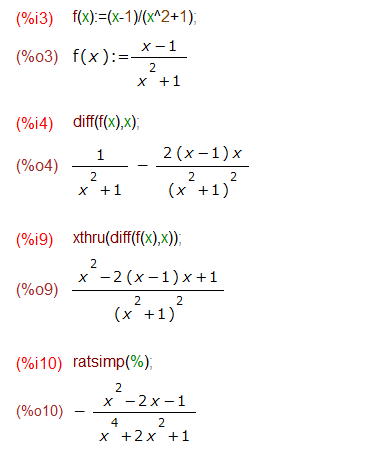上記の結果では、微分結果の形が「気に入らなかった」ので、通分のためにxthru()関数を通し、さらに分母、分子を展開して整理するためにratsimp()関数にもお願いしてみています。
さて、Mathematicaの場合、以前にやりましたが、f(x)ではなく、f[x_] と左辺の変数名にアンダースコアを付加するお約束です。例によって丸カッコでなく、角カッコです。そして、関数名の後に シングルクオートをつければ微分してくれます。
やはり通分のためにTogether[]関数を呼び出し、その後、分母のみの展開のためにExpandDenominator[]関数で展開しています。式の変形に使っている関数類についてのドキュメントは以下に
関数のお名前的には、Mathematicaの方が分かり易いと思います（個人の感想です。）ほぼほぼ同等の関数はMaximaにもそろっている筈なのですが、お名前だけ見ても作用がよく分からん感じです。慣れるしかない。
上記例で、MathematicaのD関数使わなかったのはちょっとクセがあるためです。以下のようにxで微分しろ、と指定しないと素の式をそのまま返してきます。
実際には、D[f[x],x]のようにxで微分しろ、と指定すればやってくれるみたい。
微分した結果のプロット
Maximaの場合、リストは[ ] で囲うので、wxplot2dに渡す第１引数に、元の関数と、導関数をリストとして並べて渡せば、普通にプロットしてくれます。こんな感じ。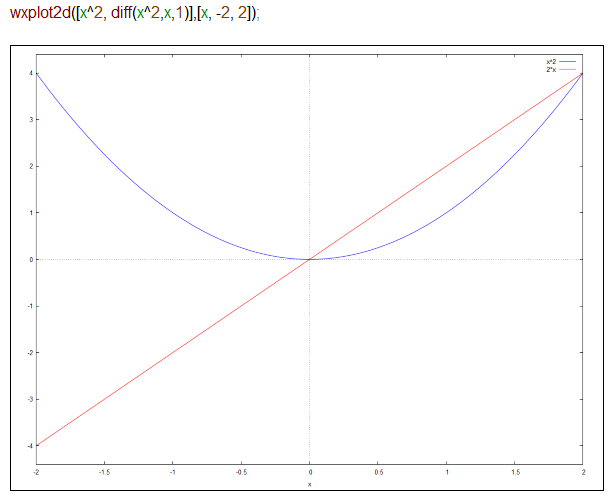
これに対してMathematicaでは以下のようにしました。Mathematicaのリストは中カッコの {} なので、基本同じスタイルではあるのです。しかし、ワザワザ関数を定義して シングルクオートで微分してみました。
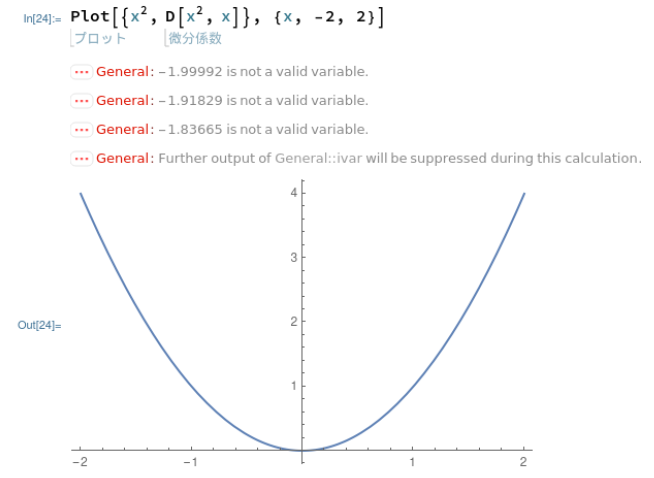
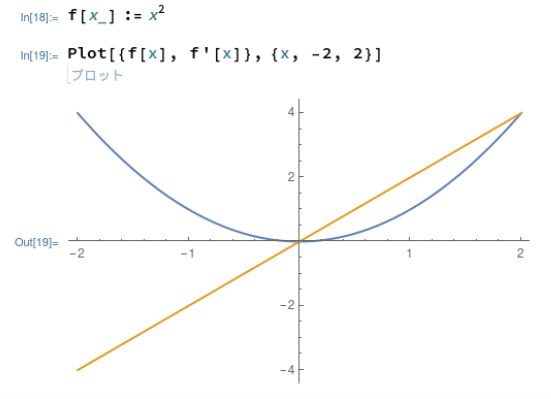そうした理由は、以下のようにD[]関数でやってみたら、なぜか以下のようにエラーがでました。元の２次関数はプロットされるのに、導関数がプロットされなかったです。何が悪いのかな～。D関数の挙動が良く分からんなあ。
まあ、一応、微分には入れた。。。