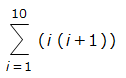数学力も無ければ、センスも無いので今回テーマには難渋しそうな予感がいたします。通例ではWolfram社Mathematicaのチュートリアルに「準拠」といいつつ準拠は進捗だけ。テキトーな例題で演習をしてました。今回は、きちっとMathematicaの例題をなぞり、その後Maximaで同じことを試みてみる、と。手探り。
※「忘却の微分方程式」投稿順 index はこちら
(文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima21.05.2です。Mathematicaはラズパイ上の12.2.0.0です。）
学生でもないのに参照させていただいておりますのは、以下のWolfram社Mathematicaのチュートリアルでございます。
まずは整数列
MathematicaもMaximaも、数列をリストとして表現することは同じでした。例によってMathematicaのリストは中カッコくくり、Maximaは角カッコ（大カッコ）くくり。
Mathematicaはリストを作成するのにTable[]を使います。余談ですが、PythonのList内包表記みたいな感じ。フィボナッチ数のような超有名なものには予め関数が用意されているのでそれをなめてリストにするのは簡単。
一方、Maximaは、そのものずばりの makelist()関数を使ってリストを生成、無骨ですが分かり易い。勿論、Maximaにもフィボナッチ数を求める関数あり、お名前は短く fib()とな。
再帰的な数列
さて、Mathematicaでは、再帰的な数列のためにReccurenceTableという関数あり、漸化式をリストの形で与えて数列を得ることができます。また、生成した数列の合計を求める関数もあり。
ううむ、MathematicaのRecurrenceTableに相当するMaxima関数を見つけられなかった私は、安易に if を使った再帰的な定義を使ってしまいました。汚い。もっとカッコいい方法があるんじゃ。でもま、定義してしまえば、そのまま makelistが使えます。また、単純なリストの合計を求める関数も分からなかったので、次の項で出てくるsum()関数で最初から求めてしまいました。
総和
総和、シグマ記号であらわすやつ、はMathematicaはSum[]、Maximaはsum()です。Mathematicaの方は、ESCキー、sumt、ESCキーで入力時点でシグマ記号を呼び出すことができるので、数式の表現としては分かり易いです（見やすいけれど、入力はメンドイ。文句を言うな、文句を。）また、一気に数式を計算してくれます。
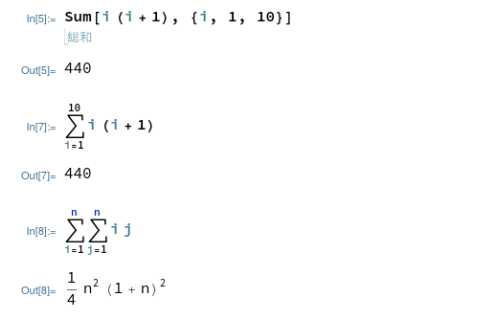
一方、Maximaでもsum()で総和が計算できますが、シグマ使った表現が欲しい場合は、シングルクウォートを使って評価を途中で止める必用があるようです。
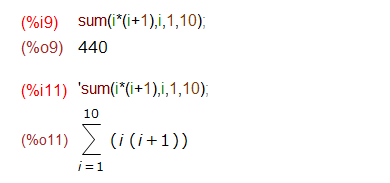
さらに、以下の例では、文字変数が入っているためか、そのままでは計算を進めてくれません。計算を進めさせるためには、制御用の大域変数 simpsumをtrueにする必要がありました。こんな感じ。
計算された式の形がMathematicaと異なったので、出力を factor()に渡して因数分解させてみました。これでようやく私にもMaximaの結果がMathematicaと等しいことが分かる。。。ホントか？
級数
Mathematicaの級数展開は Series[]です。展開させるとコマケー話の高次の項がO[]という記法で書かれます。それを切り捨てて普通の式にするNormal[]という関数あり。また、不明の関数を展開する場合は微分係数つかって展開してくれます。
Maximaの場合、テイラー展開は taylor()です。この辺のお名前の付け方がMaxima。でも内容的にはMathematicaと変わりませぬ。O[]記法の代わりにMaximaでは…となるみたい。
不明な関数の場合、微分係数で展開してくれるのも同じですが、表現の仕方が大分雰囲気違います。こんな感じ。
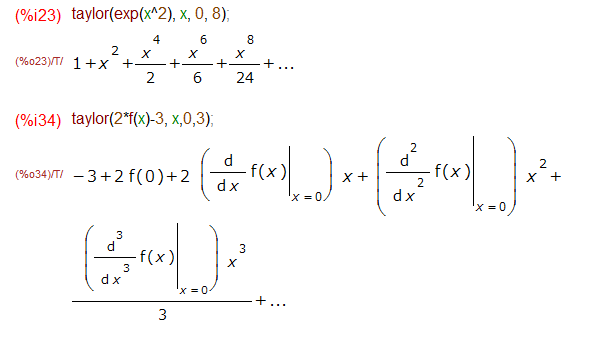Maximaの場合、テイラー展開した後に … が付いている奴らには出力のところに小さく /T/ などと書かれていて、後が「続いて」いるんだぞ感？をかもしだしてます。
途中で切り捨てて計算させる方法とか、分からないことがいろいろあるな～ また今度か？