前回は再びの２次元プロットでした。今回は３次元プロットです。テキトーでも「後はよろしく」やってくれるMathematicaと、いろいろ設定がややこしいMaxima（自分が全部制御するのだ）という「性格」の違いがでてますな。でもま、こうして３Dグラフを見ると何故か分かった気になるお手軽な私。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版）です。Mathematicaはラズパイ上の12.2.0.0です。
学生でもないのに以下のWolfram社Mathematicaのチュートリアルを勝手に参照させていただいております。
またMaximaについては、
Maxima 5.42.2 Maual: 12. Plotting
を参照させていただいております。
Maximaの3Dプロットではwxplot3dでなく、plot3dが良いと思った理由
GUIの充実した wxMaximaを使わせていただいております。2Dプロットでは、別ウインドウでGnuplotが開くplot2d()よりも、wxMaximaのノートブックの中に画像が直接埋め込まれる wxplot2d() を使わせていただいておりました。別ウインドウは面倒だから。
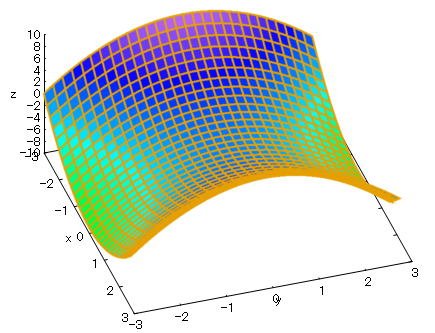
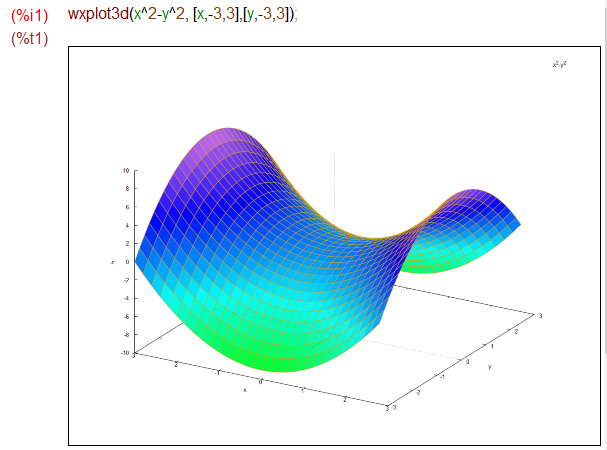
しかし、こと３Dに関しては別ウインドウで開く plot3d() の方が便利、と思います。というのは、wxplot3d() では以下のように「良い感じ」で３Dプロットしてくれるものの、「動きませぬ」。視点が変更できないみたいです。
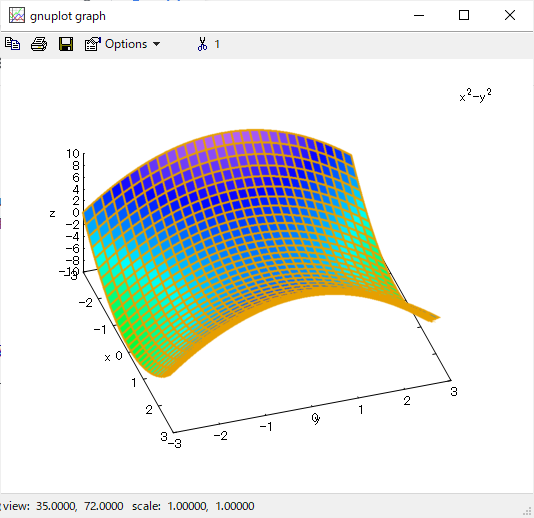
その点、以下のように plot3dを使えば
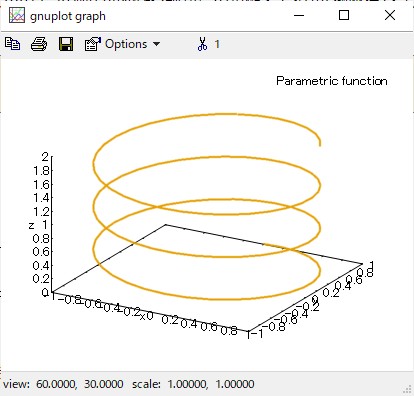
別ウインドウで gnuplot が開きます。そして「ぐりぐり」と３Ｄグラフを動かすことが可能。こんな感じ。
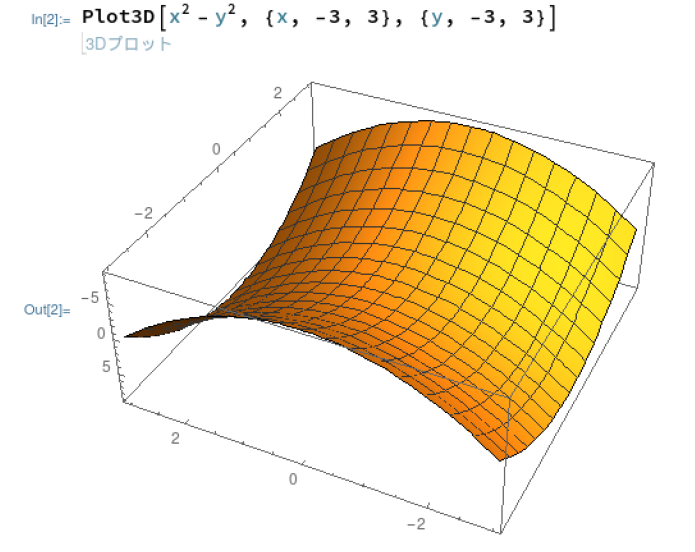
一方、Mathematicaは、Mathematicaのノートブックの中で3Dグイリグリが可能です。こんな感じ。
同じことはできるのだけれど、UI的にはMathematicaは使い易いんでないかと（個人の感想です。）
パラメトリックな３Dプロット
Mathematicaの場合、パラメトリックなプロット専用の関数があるので、それを呼んでやれば、お楽。
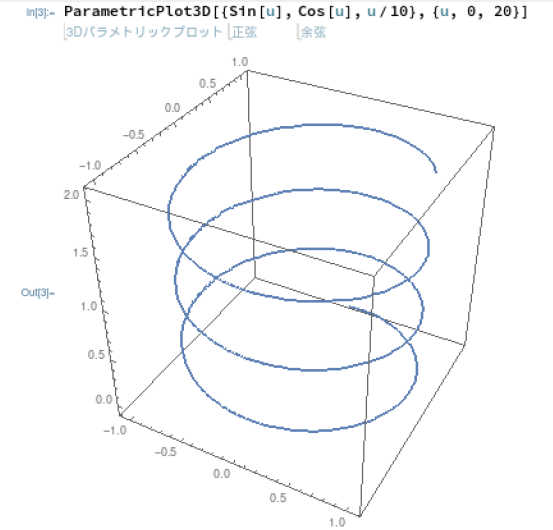
一方、Maximaのplot3dは、パラメトリックだろうが何だろうが、独立変数を２つ、従属変数１つに帰着させれば描いてくれるみたい。
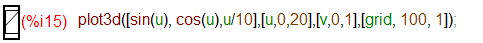上の場合、本物のパラメータ u に対して、vは単に独立変数を２個与えないとエラーになったから、という理由で付け加えたもの。ダミー。また、grid指定せず、デフォルトのままにすると「カクカク」した荒いグラフになってしまいました。
球面座標
どちらも座標系の変換はサポートしているものの、やはりやり方が異なるみたい。Mathematicaは例によって専用の命令があるので、後はよしなにでもそれなりのプロット。
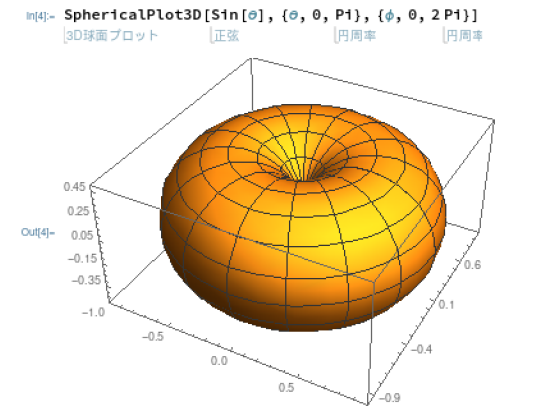
一方 Maximaは、自分でちゃんと制御するのだ、と。
上記を走らせるとこんな感じ。
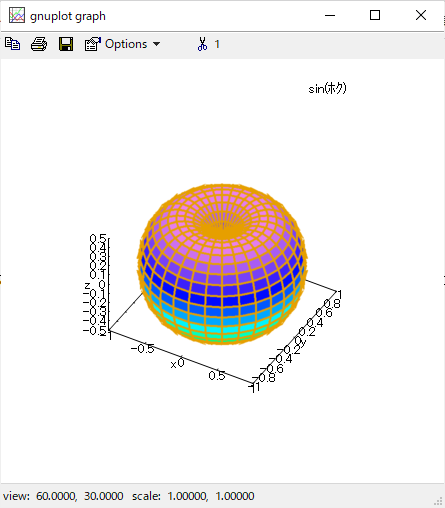
wxMaxima上では、Θとかギリシャ文字も入力できるし、使えるのですが、gnuplotの上では上図の右肩の文字列のように「化けて」しまいました。設定の方法もありそうだが、調べるのは辛そうなのでパス。thetaと綴った方が平和だな。