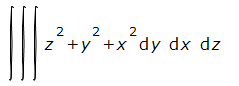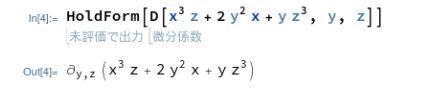第24回で微分、第25回で積分をやったですが、今回は偏微分と重積分であります。何時にもましてMathematicaの入力の「美しさ」には感動するのですが、だんだん入力が難しく（面倒に）なり、美しさの裏側には「面倒」があることに気づきます。Mathematicaの積分能力には瞠目。私が出来ないだけですが。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版）です。Mathematicaはラズパイ上の12.2.0.0です。
学生でもないのに以下のWolfram社Mathematicaのチュートリアルを勝手に参照させていただいております。
またMaximaについては、
Maxima 5.42.2 Maual: 19. Integration
を参照させていただいております。
偏微分
Maximaの場合、全微分であろうと、偏微分であろうと、diff()一本でやれるみたいです。ただ注意すべきは、１変数で微分するときは、変数名「だけ」を引数にとれば１階の微分と解釈してくれるのに対して、多変数で微分するときは、それぞれの変数の階数を並べて書いてあげないとイケないところです。
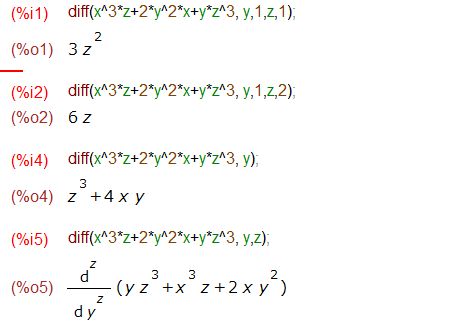
%i1の入力は、yの１階、zの１階ですが、%i2では、yの１階、zの２階です。%4iのyの１階が省略できるのに比べると、階数がある分メンドイです。また、%i5は階数を抜かして,y,zなどと書いてしまった場合の例であります。yのz階微分と解釈されてしまっています。
また、微分の式をノートに残したいときは、例によってシングルクウォートで評価を止めれば「出力」として得られます。こんな感じ。でもイマイチですな。
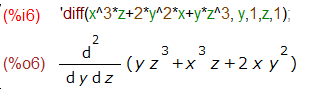一方 Mathematicaはというと、D[]で偏微分もできるのはMaximaと共通していますが、変数の指定が異なります。変数名をただ書けば「１階」と解釈してくれ、高階の場合はリスト（Mathematicaでは中カッコでかこう）で、変数名と階数を与える方式です。Maximaよりも間違え難い感じがします（個人の感想です。）
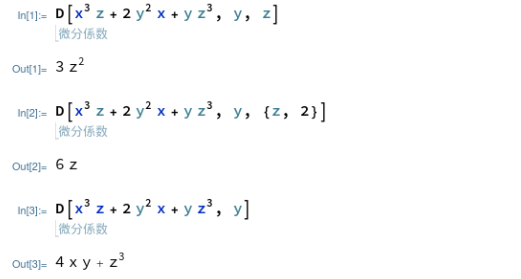微分だぞ、という式をノートに残したい場合、MathematicaはHoldForm[]に渡せば式が出力されます。こちらはちゃんと偏微分記号を使って出力されます。
Mathematicaの場合、関数であれば角カッコをとりますが、偏微分記号を使った記法では丸カッコです。どうも偏微分記号を使った記法は関数でなく、一種のシンタックス・シュガー的なものみたいに思われます。こういうのを何と呼ぶのだろ～？
重積分
Maximaの場合は、integrate()をネストしていけば重積分が可能です。以下は３重積分の例です。積分記号の表現のまま評価を中断させるには、一番内側のintegrate()にシングルクウォートをつければ良いようです。
Mathematicaの場合、入力の時点で積分記号を使った記述が可能でした。
- ＜ESCキー＞ int <ESCキー> で積分記号
- ＜ESCキー＞ dd <ESCキー> でdx などの d（なんというお名前？デルタ？）
こんな感じ。やはり積分記号の記法はシンタックス・シュガー的なもので丸カッコをとります。
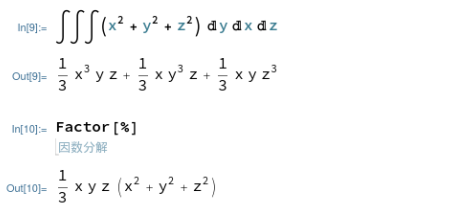
Mathematicaの以下の定積分は、計算できる筈なのですが、以下のように入力したらエラーになってしまいました。どこが悪かったんでしょうか？積分範囲の指定の方法が悪いの？
そこで、ベタにIntegrate[]関数を使って書き直してみました。こちらは問題なく積分できました（わたしゃ自分ではできないです。）
上記のケースをMaximaでも真似して解こうとしましたがエラーで落ちました。原因不明であります。