前回はデータフレームだったですが、今回は久しぶりに時系列データ、それもマルチプルなやつ、に戻ります。ggplotのお陰で美麗なグラフを描けるようになったので今回も適用っと思ったら、時系列データには直接作用できないみたい。要変換ってことか。それにしてもスイスってEUじゃなかったろ~、気になる。
※「データのお砂場」投稿順Indexはこちら
今回のやっつけでご乱心なターゲットは、EuStockMarketsという英独仏スイスの株式市場のインデックスの時系列データのサンプルです。1990年代のもの。この年寄りは十分最近に感じますが、若者には古代のデータかと。
処理を始める前にちょっと気になったのが、スイスってEUじゃないのにEU扱いされているじゃん、という点。かなり引っ掛かりましたぜ。しかし、どうも聞くところによると、
スイスはEU加盟国ではないのに、2021年にEUから離脱した
らしいです。華々しいブレクジットの影でスイスもだったのね。その辺の経緯については、ジェトロ様の以下の記事がありましたのでURL貼り付けときます。
どうもスイスがEU扱いされるような条約などがいろいろあったってことらしく、このサンプルデータセットがスイスを含めたのにも根拠がある?ホントか?
EuStockMarketsサンプルデータセット
このデータセットについての解説は以下にあります。
Daily Closing Prices of Major European Stock Indices, 1991-1998
データの出所など、必要最小限の説明はありますが、処理例みたいなことは書かれていません。自分で考えてね、みたいな。
まずは生データ
まずはサンプルデータをロードして、データの形式を確かめるところから。
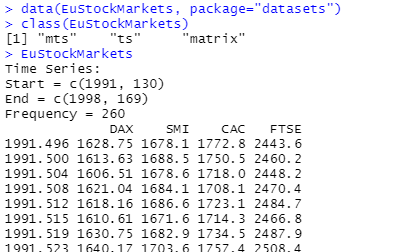
mts とあるのは多変量時系列ということらしいです。そのデータ実体はと言えば、1860行 x 4列 の行列(matrix)に格納されているようです。時を与えるのは、Start-End間の一連の数列であり、Frequency=260ということから1年は260Hz?(周期)、その1991の130周期目のデータから1998年の169周期目までと理解。そういう解釈で良いのかな?
実体的には、株式市場がお休みの日もあるので、営業日のみをカウントして260になるのだと思います。毎年同じ日数になるの?という疑問もあり。なお、
- DAX ドイツ
- SMI スイス
- CAC フランス
- FTSE イギリス
のそれぞれ株価指数みたいです。
データのプロット
前回、前々回と ggplot2 の威力に感動していたので、何も調べもせず ggplotにこのデータを食わせてみました。
![]()
駄目でした。データフレームかfortify()できるオブジェクトでないとダメじゃ、mts形式のS3オブジェクトは無理って感じですかい。S3オブジェクト出てまいりました。遥かな昔にちょいと勉強したことがあったです。Rのオブジェクト指向、Rのクラス。S3というのは確か古い形式だった筈。おいおい勉強しなおして、データを変形する方法を学ばないと ggplot2の恩恵には浴せないっと。
手っ取り早く昔ながらの方法?をとってみました。
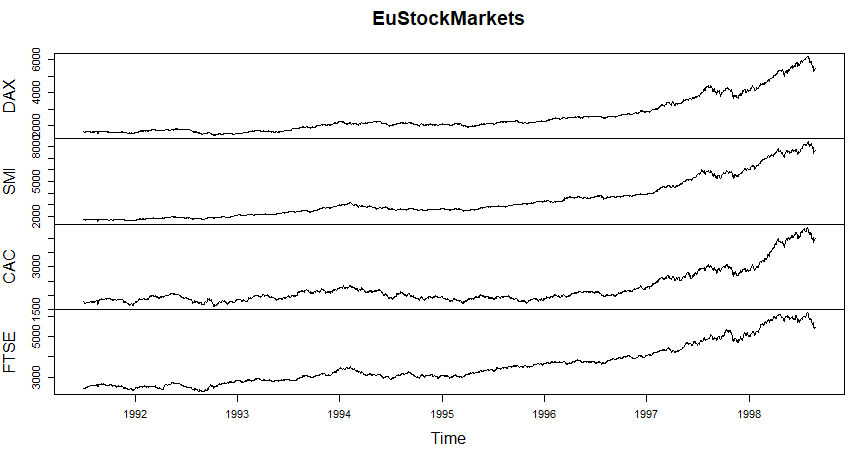
plot(EuStockMarkets)
シンプルなコマンドですが、効きましたぞ。ちゃんとデータ構造を見て、それなりの処理をしてくれます。こういうところがRのオブジェクト指向?
とりあえずデータの全体像は浮かび上がってまいりました。しかし、色気がないです。なんとか色をつけられないものか。やってみました。
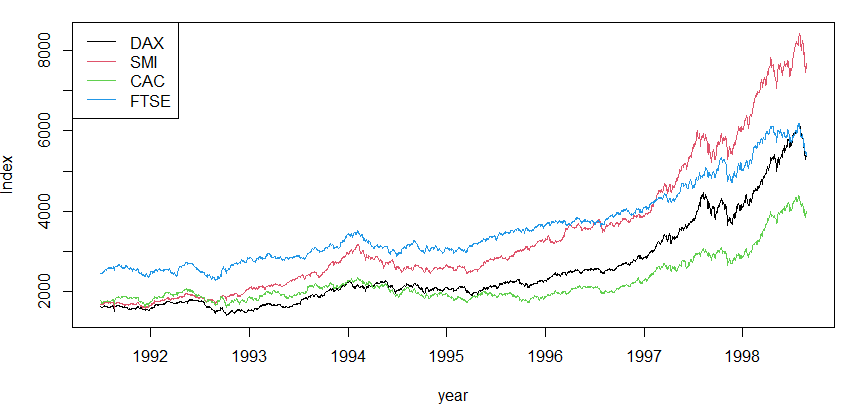
ts.plot(EuStockMarkets[,"DAX"],EuStockMarkets[,"SMI"],EuStockMarkets[,"CAC"],EuStockMarkets[,"FTSE"],gpars=list(xlab="year",ylab="Index", col=c(1:4)))
legend("topleft",c("DAX", "SMI", "CAC", "FTSE"),lty=c(1,1,1,1),col=c(1:4))
上記のコマンドの結果を冒頭のアイキャッチ画像に貼り付けました。色がついておりますぞ。
相互相関を観察
本日の日経平均は大分下落してガッカリです。各国の指数に相関関係があるのは皆さんよくご存じと思います。上記のグラフを観察してもその動きはクリソツ。多分、相互相関をとったらかなり「よい感じ」になるのではないかと。やってみました、スイスとフランス。
ccf(EuStockMarkets[,"SMI"], EuStockMarkets[,"CAC"])
この結果得られたグラフがこちら。
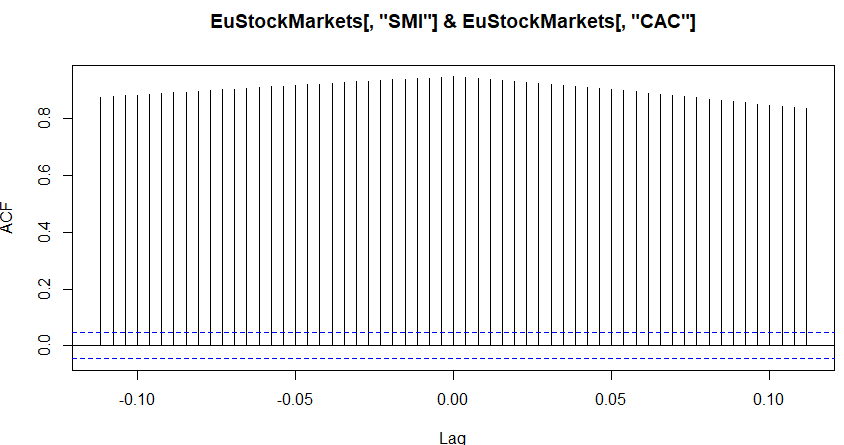
値は0.9くらいなので、相関は強いっと。そしてJUST TIME。当たり前だけれども。
Rのオブジェクトとか、多変量時系列とか調べなければならないことが分かったので、本日はここまでとさせていただきます。