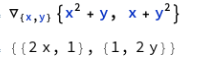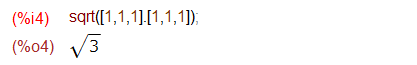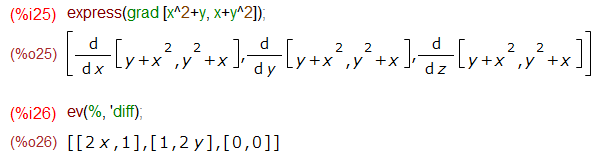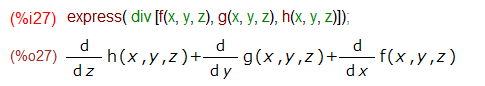前回、偏微分と重積分だったので、今回はベクトル解析であります。何時にもまして感じますのが、分かり易いお名前の専用関数があり「お任せ」で処理してくれるMathematicaと、計算のやり方を知って「さえ」いれば計算が出来るMaximaのスタイルの違いであります。私のように高校レベルの公式すらおぼつかないものにはMaximaキツイ。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版）です。Mathematicaはラズパイ上の12.2.0.0です。
さて、以下のWolfram社Mathematicaのチュートリアルを勝手に参照させていただいております、学生でもないのに。
数学を学ぶ学生のための入門チュートリアル ベクトル解析と可視化
今回は、上記ページにあるMathematicaの処理例を動かしてみながら、同じことをMaximaでやるにはどうしたらよいか考えてみた、という通例のスタイル。
内積と外積
Mathematicaは中カッコ、{ }で囲うとリストになります。そしてリストすなわち、ベクトルとしても使えるみたい。 ベクトルに対しては、数学の記法どおり、”.” 「ドット」が内積、”ｘ” 「バツ印？」が外積として働く。こんな感じ。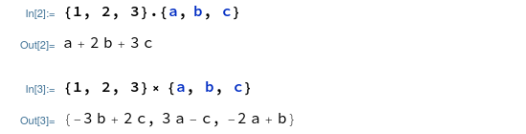
なお、外積の「×」印は、例によってESCキー使った記法で入力です。以下のごとし。
ESCキー cross ESCキー
ただのｘではありませぬ。
一方Maximaでは、大カッコ（角カッコ）、[ ] で囲うとリストです。そして、やはりリストはベクトルとしても使えるみたい。ただ、内積のためには “.” が使えるのに、外積は差別されていて？演算子が用意されてないみたいです。定義に従って要素毎に取り出して演算する関数を定義すればいいだろ～ってことかい？ちとカッコイイ方法を見つけてしまいました。
カッコ良すぎて、私にはピンときません。余因子行列を転置して３行目を取れと。
最初からMaximaキツイな。
ベクトルのノルム
さてベクトルのノルムです。Mathematicaは、そのものずばりの関数があるので、それにベクトル（リスト）を引数に与えれば計算してくれます。
またもや、ですがMaximaではそのものズバリの関数が見つかりませんでした。流石に私でもノルムの計算の仕方は知っているので、その通りに書けば結果が得られます。後で norm() という関数に定義しておくことにしましたが。
ベクトルの射影
つぎは正射影です。最初のベクトルを２番目のベクトルに正射影すると。これまたMathematicaには、そのものズバリの関数があるので、お任せするだけ。らくちん。
例によって、Maximaではそのものズバリの関数が見つからなかったので、見よう見まねで projection()関数を定義してみました。とりあえず上と同じ結果は出ましたが、本当に大丈夫なのか？
私のように記憶の弱った（最初から覚えてない。。。）年寄りには「お任せ」がありがたいです。
ベクトルのなす角
これまた Mathematicaには、分かり易いお名前の専用の関数があるので、「お任せ」するだけです。分かり易い分、ちょっとお名前が長いのはいたしかたないかと。
しかし、Maximaではそうはいきません。先ほどのnorm()と内積とあわせて角度を求める関数（どこまで正しく動くのだか不明）を定義してみました。まあ、とりあえず計算例は計算できているみたいだな。
グラディエント（gradient)、勾配
Mathematicaでは、再び ESCキーをつかった記法が登場です。
ESCキー grad ESCキー
で「ナブラ」演算子が現れます。下付きの添え字と本体の２個のハコも現れるので、以下のように入力すればOK。スカラー場に対してこの演算子を適用すれば「勾配」が求まるのだ、と。昔習ったような、記憶違いのような。
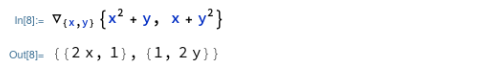
ここに来て、Maximaの方はいよいよ煮詰まって？きたので、標準で付属しているライブラリファイルに頼ることにいたします。こんな感じ。
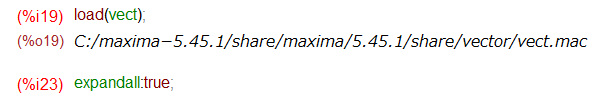
すると「前置式演算子」として grad とか div とかが使えるようになるのですが、この使い方がなかなかムツカシイです。なんだか多数のフラグがあって、勝手に動作しないように、鍵かけてあったりするのです。よくわかっていて、どこまでで「止めたい」という明確な意思がある人にとっては必要な機能だと思います。しかし、「お任せ」でお願いしたい私には過ぎたるものであります。
唯一使えそうだったのがこちら。express()関数に渡して「名詞形」の表現にしてから、おもむろに評価(ev関数)してもらう方法。偏微分記号が出てこないのがちょっと残念。
ダイバージェンス（divergence)、発散
さて、Mathematicaには 専用の関数あり。解析対象のベクトル場を与えるつもりでリスト{f, g, h} を与えれば計算してくれる(といっても実体ないから形だけだけれども）と。
Maximaでも、先ほどライブラリをロードしてあるので、前置演算子 div が使えるようになってます。先ほど同様、express()方式？でえいやー。やっぱり偏微分演算子のシンボルが無い？らしいのが残念。
ベクトル解析、その２へ続くだな。