前回に引き続き、課題『母音の音声合成器』を手習ひしてまいりたいと思います。今回は「声道に対応する共振器」であります。今回もマイコン上での実習はお休みで、Scilab使って共振器の特性を調べてみたいと思います。Scilab使ってとは言うものの、Scilab素人の私には過ぎたる野望か。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
勝手に手習ひさせていただいております教科書へのリンクを以下に記します。
三上直樹先生著、工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
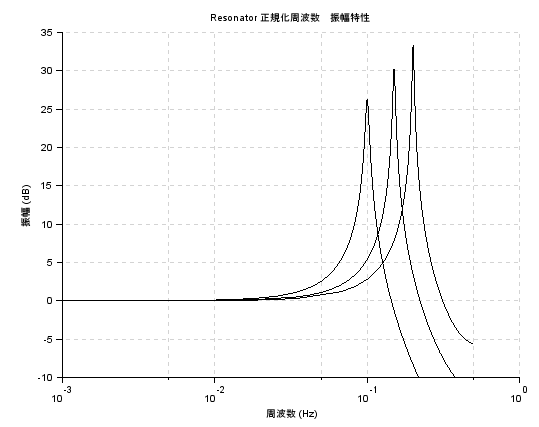
上記の御本ではさらっと1ページ半ほどで通り過ぎている「声道に対応する共振器」が本日の手習ひのテーマであります。ぶっちゃけ、
図5にしめされている振幅特性のグラフを自力で描きたい
という希望(野望)でございます。
共振、つまりはフォルマント
人間の音声に「フォルマント周波数」なるものがあることを知ったのは、遥か40年ほど昔のことでありました。当時「新入のペーペー」だった私は、上司の人から、ある8ビットマイコンでDTMF音声を生成できないか調べよ、という課題を与えられました。DTMFって何ってところから調べ始めたのです。DTMF = Dual-Tone Multi-Frequencyです。プッシュ回線の電話機で「ピ、ポ、パ、ポ」などと発せられる音であります。当時は、ダイアル回線からプッシュ回線への移行期でDTMFの生成に需要があったのだと思います。
DTMF、物まねで「ピ、ポ、パ」などと口で発音しても信号は通らない筈。人間が発音するときに現れる、ホルマント周波数の組み合わせを調べあげ、普通の人では発音できないような周波数の組み合わせであの音を出しているのです。DTMF作れという課題は沙汰やみとなり、その方面にはとんと縁が無いまま、ホルマント周波数のことも長らく忘れておりましたが、この度思い出しましてございます。
というわけで(どういうわけだ?)複数の周波数が「混ざっている」のが人の声であります。そしてその周波数は声道が共振器となって発生する、と。
普通の人は、第1、第2ときて第3フォルマント周波数ともなると微妙。声が良い歌手の人であると第Nフォルマントまで鳴り響いておるとの噂です。閑話休題。
共振器のブロックダイアグラム
さてデジタルで共振器を作るためのブロックダイアグラムを三上先生の教科書から引用させていただきます。こんな感じ。
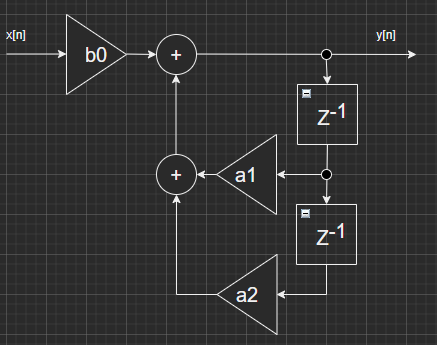
これが一つの周波数に対応するので、これを日本語の母音5つに対応する組み合わせだけ繋げていけばフォルマントが得られるということであります。
教科書には、a1, a2 そして b0を求めるための式が掲載されとります。また、上のブロックダイアグラムを見れば明らかですが、伝達関数 H(z) も記載ありです。
よってa1, a2, b0を求める条件を入れたら、共振器の特性(ボード線図)を計算できる筈。教科書には、共振周波数 1kHz, 2kHz, 3kHzで共振帯域幅50Hzのときの振幅特性のグラフが記載されています。任意の共振周波数での特性が得られるよう、Scilab使ってみるべし、と。
作製したScilabコード
作製したScilbabのコード、ささやかなものですが、結構時間かかりました。参照させていただいたマニュアルページなどを以下に列挙しておきます。
syslin 線形システムを定義する。連続時間システム、離散時間システム対応
clc;
clear();
clf;
function [a1, a2, b0]=ResonatorParam(F0, B0, Fs)
// F0 : 共振周波数,B0 : 共振帯域幅,Fs : サンプリング周波数
piT = %pi/Fs
a1 = 2*exp(-piT*B0)*cos(2*piT*F0)
a2 = -exp(-2*piT*B0)
b0 = 1.0 - a1 - a2
endfunction
[a10, a20, b00] = ResonatorParam(1000, 50, 10000)
[a11, a21, b01] = ResonatorParam(1500, 50, 10000)
[a12, a22, b02] = ResonatorParam(2000, 50, 10000)
H0 = syslin('d', (b00 / (1 - a10*%z^(-1) - a20*%z^(-2))))
H1 = syslin('d', (b01 / (1 - a11*%z^(-1) - a21*%z^(-2))))
H2 = syslin('d', (b02 / (1 - a12*%z^(-1) - a22*%z^(-2))))
bode([H0; H1; H2], 0.01, 1.0, ['H0'; 'H1'; 'H2'])
xtitle("Resonator 正規化周波数 Bode線図")
最初の方にあります function定義は、a1, a2, b0の係数を求めるための関数です。上記のサンプルプログラムでは、以下のパラメータで係数を求めています。
-
- H0 共振周波数1kHz、共振帯域50Hz、サンプリング周波数 10kHz
- H1 共振周波数1.5kHz、共振帯域50Hz、サンプリング周波数 10kHz
- H2 共振周波数2kHz、共振帯域50Hz、サンプリング周波数 10kHz
さて、伝達関数H(z)は、syslin()関数に離散時間システムである’d’というお印とともに、%z(見やすいようにzを%zの代理にする方法もあるようですが、デフォルトで使用できる%zを使いました)で記述した式を与えれば定義が可能です。
後はボード線図を描く bode()関数にこの離散時間の伝達関数を渡せば特性を描いてくれますが、描いてみて気づいたことは
離散時間では、サンプリング周波数を1Hzとみなした「正規化周波数」で計算される
ということみたいです。連続時間(%sで記述し、syslinには’c’を指定)であれば、普通に実周波数で計算してくれるみたいです。しかし離散時間には一線が設けられている?ですぜ。
なんとか実時間風に「デコレーション」できないかとちょっと調べたのですが分かりませぬ。今回はパス。トホホ。
作製したボード線図
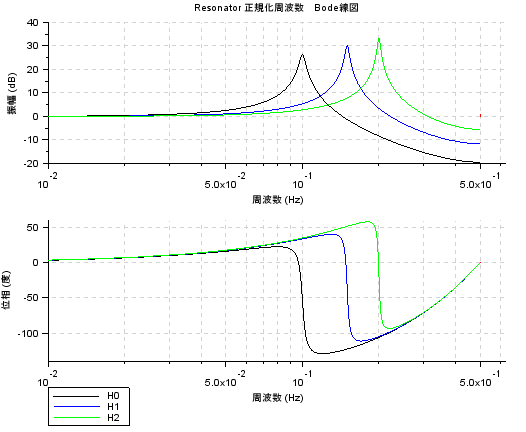
アイキャッチ画像にはゲインのみのグラフを掲げましたが、上記のプログラムで生成されるのは、振幅と位相の両方からなるボード線図です。横軸の周波数は、サンプリング周波数を 1Hz とみなす「正規化」されたもので、かつ、ナイキスト周波数以上は無駄ということからか、0.5Hz位置でバッサリ切られて出力されます。上記のパラメータとの対応だと
- H0 黒
- H1 青
- H2 緑
教科書とは設定した共振周波数が違いますが、「予定どおり」な雰囲気。
共振特性、自力で計算できるような気がしてきた(錯覚だよ、多分。)