一度道筋がついてしまえば、以下同文方式。Scilab使って特性を調べるのは簡単に思えてきました（本当か？）ターゲットは『母音音声合成器』第３の要素「高域強調器」であります。こいつは「口からの放射」に対応とのこと。手習ひさせていただいております教科書どおりの特性が計算できればOKっと。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
まずは勝手に手習ひさせていただいております教科書へのリンクです。
三上直樹先生著、工学社『「Armマイコン」プログラムで学ぶデジタル信号処理』
前回は「声道に対応する共振器」でしたが、今回は「口からの放射に対応するフィルタ」部分の特性を計算して「図７」のような振幅特性が描ければよい、と。ま、計算といっても、実際にやってくれるのはScilabなのですが。
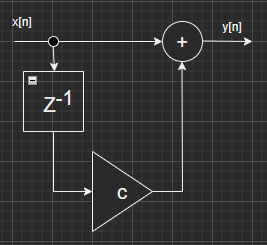
高域強調器のブロックダイアグラムと伝達関数
冒頭のアイキャッチ画像にブロックダイアグラムを掲げさせていただきました。「とてもシンプル」なFIRフィルタであります。そして伝達関数は以下です。
R(z) = 1 – c*z-1
前回のようにパラメータを求めるのに関数がいるわけでもなく、いくつかのc値に対して振幅特性が求まればよいのであります。
Scilabコード
三上先生の教科書のグラフと同じく、３種類の c 値、0.5、0.8、1.0で計算してみましたが、プログラムというほどのプログラムにもなりません。
// Radiator
clc;
clear();
clf;
c0 = 0.5
c1 = 0.8
c2 = 1.0
R0 = syslin('d', (1-c0*%z^(-1)))
R1 = syslin('d', (1-c1*%z^(-1)))
R2 = syslin('d', (1-c2*%z^(-1)))
bode([R0; R1; R2], 0.01, 1.0, ['c=0.5'; 'c=0.8'; 'c=1.0'])
xtitle("Radiator 正規化周波数 Bode線図")
計算結果
結果のボード線図が以下に。前回にづづき、離散時間のプロットなので、サンプリング周波数を1Hzと「正規化」した周波数にて、上限0.5Hz(ナイキスト周波数）までのグラフとなっております。
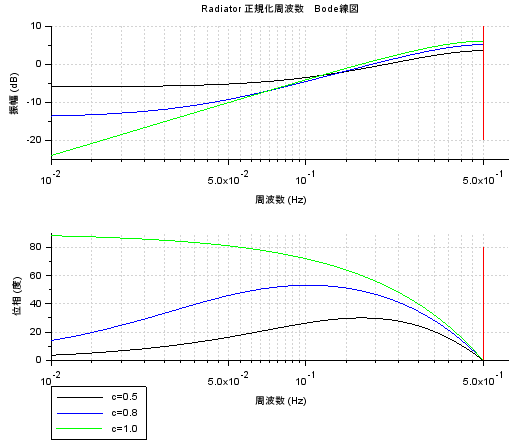10-1 のところが実時間の 1kHzにあたります。高い周波数になると「強調」されているのが分かります。一方、低い周波数は減衰しますが、その程度はcが大きくなるほど大きくなるみたい。
ようやく部品３つの「計算上」の吟味が出来た（ホントか？）ので、次回は、久しぶりに実機 STM32F446を取り出して、現物で実験したいと思います。しかし、よく考えると「音」の実験だし、スピーカつなげて音を出したいよね。そういえば、昔スピーカ・アンプを用意してあった気がする。どこいった？あれ。