ABC順に端から「当たって」いるので、よく分からない分析手法が登場するのは当然です。今回は因子分析(factor analysis)とな。サッパリ分かりません。ターゲットのデータセットは「7歳から17歳までの305名の girlsの物理計測8種データの分散共分散行列」です。girlsは良いが、分散共分散行列とは何者。
※「データのお砂場」投稿順Indexはこちら
まずはデータセットから
データセットについての解説ページのURLは以下です。
Harmanというのは、このデータが掲載されている1976年の御本の著者のようです。2.3というのは、その本の Table 2.3のデータだからみたいです。
データそのものは、8x8の分散共分散行列なので、個人を特定できる情報などまったくなく、個人情報もプライバシーも問題なさそうではあるのですが、今日的には、データ収集する時点でとても難しい問題に直面するような気もいたします。
まずは生データを
データをロードして構造をみてみると以下のように list です。これは構造の異なる複数の要素を中に格納しているから、コンテナみたいな使い方ですかね。メインとなるデータは、$covという名で格納されている分散共分散行列?です。この実体はmatrixでした。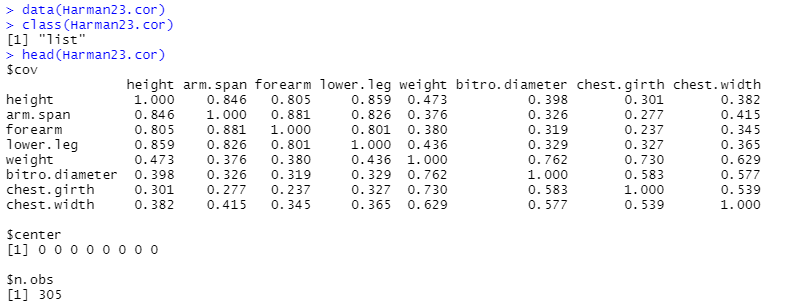
この8x8の行列、対角成分は全て1.0です。非対角成分はそれぞれの「変数」の間の相関関係をあらわしているみたい。知らんけど。
それぞれの「変数」は以下です。別に邪な心で書くわけでないのでご承知おきください。
- height 身長
- arm span 指端距離
- forearm 前腕
- lower leg 下腿
- weight 体重
- bitro diameter (bitrochanteric diameterの事ではないか?)臀部横径
- chest girth 胸囲
- chest width 胸幅
とりあえず日本語にしてみたけれども。
早速因子分析
R言語の関数 factanal は、最尤法による因子分析関数であるらしいです。「因子負荷量(factor loading)」をあらわす行列を求めてくれるらしい。まずは、例題に書いてあるとおりの因子1個とした場合の処理。
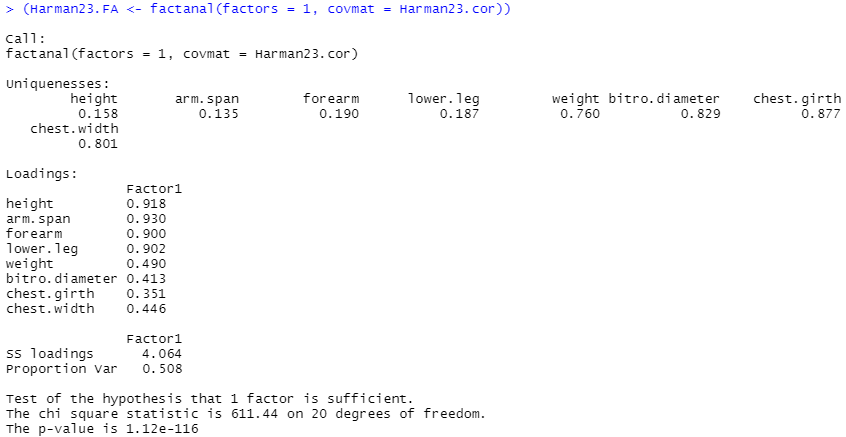
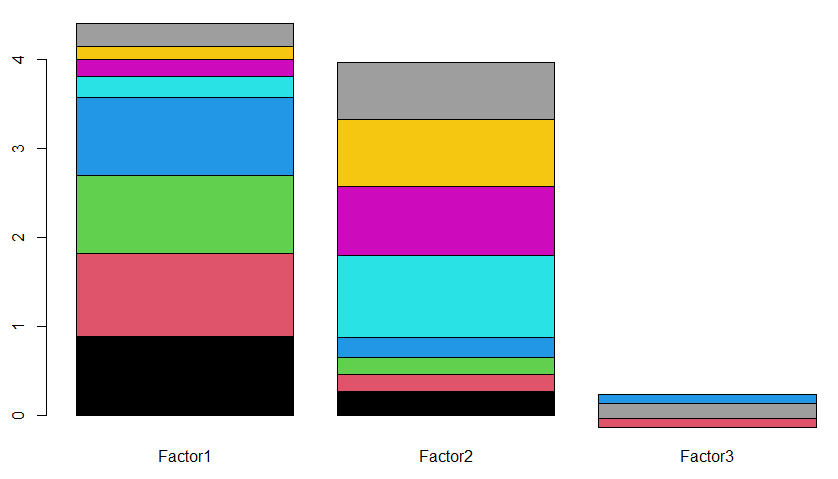
因子1個の後は、勝手に因子を2個、3個と増やし、その度に棒グラフにして、「因子負荷量」なるものの重みを見てみました。こんなコマンドラインで。
> barplot(Harman23.FA$loadings) > Harman23.FA <- factanal(factors = 2, covmat = Harman23.cor) > barplot(Harman23.FA$loadings) > Harman23.FA <- factanal(factors = 3, covmat = Harman23.cor) > barplot(Harman23.FA$loadings)
3個のときの棒グラフに色を付けたものを冒頭のアイキャッチ画像にかがげました。色付きにする場合の描き方は以下に。
barplot(Harman23.FA$loadings, col=c(1,2,3,4,5,6,7,8))
ファクタ2つ目までは勝手ながら「良い感じ」に見えます。3つ目はイマイチかね。このような方法であると、8つの変数のうち、前半4つは「骨格」の長さに関係するように思われ、ファクタの1つ目がそれらを代表。一方後半4つは「肉付き」に関係するように思われ、ファクタの2つ目がそれらを代表。結局、一つ目は身長、2つ目は体重を代表とする2大グループがあることは明らかではないかと。ホントか?感覚的にはそんな気もしますが。
3ファクタのときの計算結果がこちら。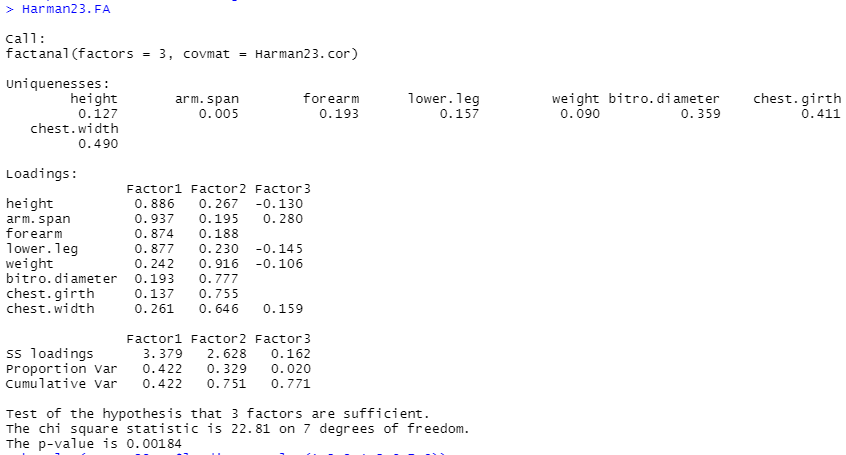
実際には、ここに「回転」的な変形を加えて、共通因子を探していくみたい。ちょっと何言っているか分からないので、今回はここでおしまいとしとうございます。でも、またすぐハーマンさんが出てくるみたい。アルファベット順だから。