今回も米国の古い時代のデータです。戦前（第２次大戦ですぞ。応仁の乱でもウクライナ戦争でもありませぬ）から戦後にかけての米国の消費支出のデータらしいです。戦後の「順調な拡大」が読み取れる一方、米国といってもまだまだエンゲル係数高そうな感じです。今と比べると大分様子が異なります。だいたいタバコが重要な支出となっているし。
※「データのお砂場」投稿順Indexはこちら
さてはて、R言語所蔵のサンプルデータをABC順（大文字先）で端から眺めております。今回のサンプルデータセットUSPersonalExpenditure の説明が以下のページにあります。
５年毎、といっても１９４０年から１９６０年までの古い米国の統計資料です。１９４０年時点では米国はまだ第２次世界大戦に参戦しておらず「戦前」。１９４５年が「終戦」の年で、その後の経済拡大期のデータが３点ということになります。
データ項目は以下の５項目ということです。
-
- Food and Tobacco
- Household Operation
- Medical and Health
- Personal Care
- Private Education
各項目の内訳は分かりませぬ。ぱっと見、なんとなく分かる気もするのですが、個別にみて考えると何だかよく分からない分類ですな。１番のFood and Tobaccoだけは分かり易いです。しかし食費とタバコ代？この時代はまだタバコ代が大きな割合を占めていたのでしょう。現代とはだいぶ様相が異なります。
各項目の数値はビリオンダラーです。まさか世帯や個人毎の平均ではないでしょう。米国全体での消費支出を足し込んだ値だと想像できます。しかし現代的な規模感からするとかなり「小さい」数字です。
まずは生データ
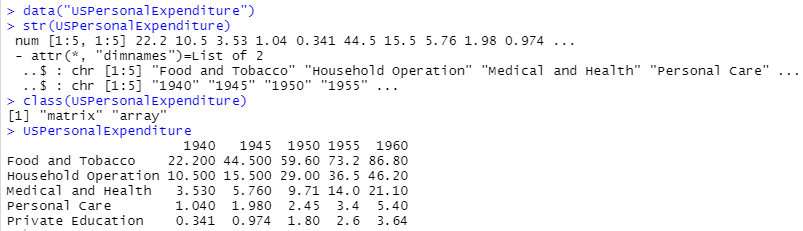
いつものように生データをロードして調べてみたところが以下です。
５ｘ５の行列データでした。行方向に項目がとってあり、列方向に年が記されています。
ただ、列方向に時間という形式だと、時間経過にたいしてのグラフが描きにくいように思いました。私がRを使いこなせていないためですが。
エイヤーで転置した後、pairsに各項目間の関係性をグラフ化してもらいました。こんな操作で。
dataT <- t(USPersonalExpenditure) pairs(dataT)
グラフは以下です。基本どれも右肩上がりで正の相関がとれそうです。ただ、データ組によっては１９４５年に相当するポイントのところで「折れ」が発生している感じです。これは第二次世界大戦が与えた影響でしょう。他の支出を削って食費に回した？感じがします。それでも、この程度の「折れ」の痕跡しかない米国の巨大さ。戦後は順調に全項目とも拡大基調が見てとれます。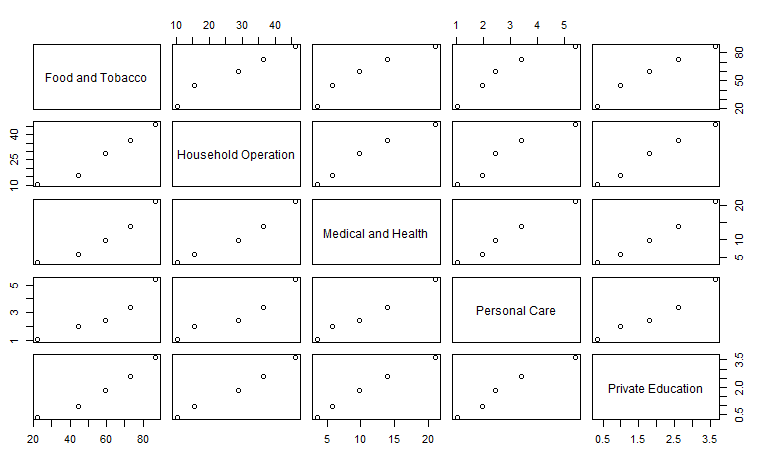
対時間経過でグラフを描きたいと思ったのですが、行列形式のままだと私は上手く描けなかったのでさらに変形してしまいました。処理は以下です。
year <- dimnames(USPersonalExpenditure)[2] df <- as.data.frame(dataT)
きっとPlotももっとカッコイイ方法があるのだと思いますが、力ずくです。こんな感じ。
plot(df$`Food and Tobacco`, col=1, type="o", xlim=c(1,5), ylim=c(0,100),
xaxt="n", xlab="year", ylab="Billion US dollars", main="USPersonalExpenditure")
par(new=T)
plot(df$`Household Operation`, col=2, type="o", xlim=c(1,5), ylim=c(0,100), xaxt="n", ann=F)
par(new=T)
plot(df$`Medical and Health`, col=3, type="o", xlim=c(1,5), ylim=c(0,100), xaxt="n", ann=F)
par(new=T)
plot(df$`Personal Care`, col=4, type="o", xlim=c(1,5), ylim=c(0,100), xaxt="n", ann=F)
par(new=T)
plot(df$`Private Education`, col=5, type="o", xlim=c(1,5), ylim=c(0,100), xaxt="n", ann=F)
par(new=T)
axis(1, at=1:5, labels=year[[1]])
legend("topleft", legend=
c("Food and Tobacco", "Household Operation", "Medical and Health", "Personal Care", "Private Education"),
lty=1, col=1:5)
上記のプロットの結果が以下です。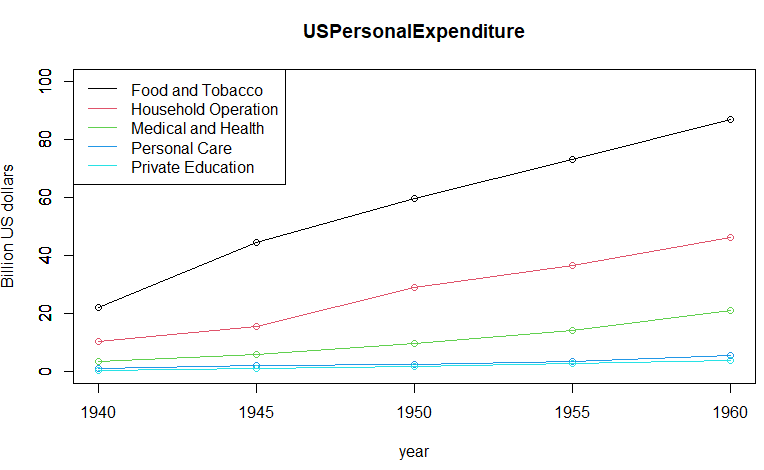
力ずくの割には変哲の無いグラフだね。
medpolish
さてサンプルデータセットの説明ページには、今回処理例の記載がありました。medpolishという処理をせよ、とのことです。
Median Polish (Robust Twoway Decomposition) of a Matrix
勝手な理解で書かせてもらうと、今回のような２次元のデータテーブルから線形の回帰方程式を取得するための方法のようです。ホントか？
回帰は、行、列の両方向に対してで、各データは、
overall + 行の効果分 + 列の効果分 + 残差
みたいな表現となるようです。なお推定するときに中央値（Median)を使うので、平均値を使う方法にくらべると外れ値などによる影響は少ないらしいです。知らんけど。
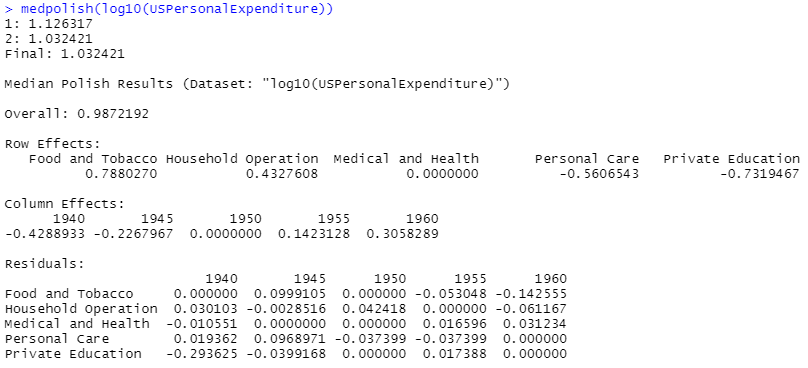
素人には良く分からんのですが、Rに計算はお願いできます。行列双方向なので元データそのままズバリです。こんな感じ。
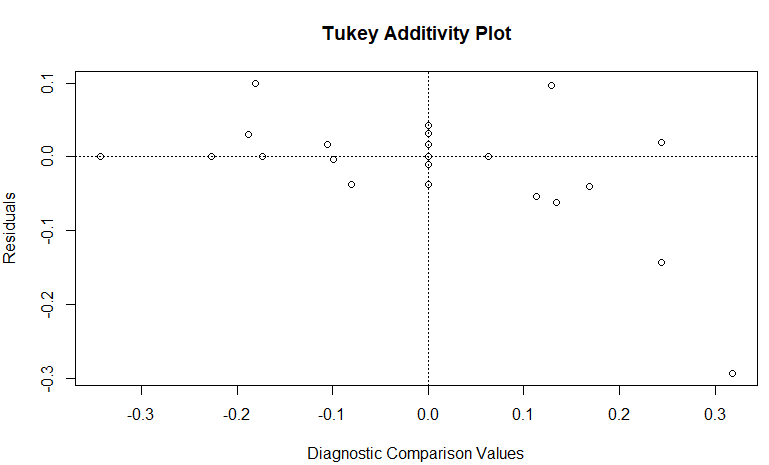
処理例には無いのですが、この結果を plot に与えてみると Tukey Additivity Plot なるものが出力されました。Tukeyは、この手法を開発した先生のお名前みたいですが、後はサッパリです。上記の解析結果を吟味するためのプロットなのでしょうが、何だかな～。
今回も分からぬままに、たった２５点のデータの大海に沈みました。