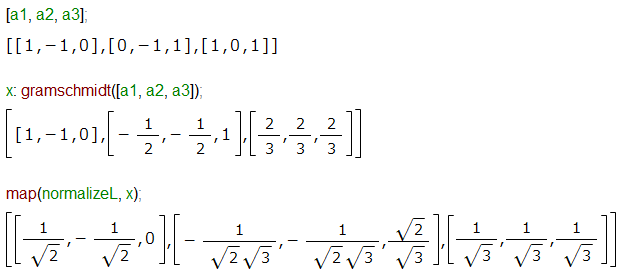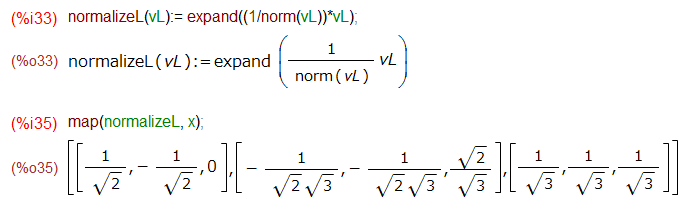前回は「数学風?」列ベクトル表記にこだわって処理してみましたが、今回、早くも列ベクトル断念。やりたいことにピッタシの関数があったのですが、処理は行単位デス。行ベクトルというかリスト表現のままの方が処理は簡潔に書けますものね。それでグラム・シュミットの直交化法じゃ、と。
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習?は、WindowsPC上の以下のバージョンで行わせていただいております。
-
- wxMaxima 21.05.2 (MaximaのGUIフロントエンド的なもの?)
- Maxima 5.45.1
※以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
数学の御本なのに数学の勉強には全然なってないです。恐れ多いことです。
直交化、正規直交化
さて今回のお題は「3つの列ベクトルa1, a2, a3で与えられるR3の基底 {a1, a2, a3} を正規直交基底 {u1, u2, u3} に変換せよ」というものであります。a1, a2, a3には具体的な数値が示されとります。上記教科書では『シュミットの正規直交化法』の練習ということになっております。
教科書的には、a1からまずu1を求め、求めたu1とa2からu1と直交するb2を求め、それを正規化してu2を求め、という塩梅で、順ぐりに1個づつ計算していく方法が示されています。
今回は、まず教科書の方法通りに計算(といって計算するのはMaxima様ですが)してみます。続いてMaximaの eigen パッケージ内のグラム・シュミットの直交化法の関数を使って同じことを行ってみます。
まず1点、以下の筑波大の方ページから1か所引用させていただきます。
内積空間Vにおいて,ある基底を直交基底にすることを直交化(orthogonalize)という. 正規直交基底にするときは正規直交化(orthonormalize)という.
今回のお題は、orthonormalize せよという課題ですが、Maximaのパッケージでは、orthgonalize用の関数が定義されとります。
直交化はやっちゃるから、正規化くらいは自分でやれよ
ってな感じでしょうかね。
Maximaでのグラムシュミットアルゴリズム
使用方法は、以下の日本語Maximaマニュアルページ(東北大)に書かれておりますぞ。
23. Matrices and Linear Algebra
eigenパッケージのロードが必要です。
load(eigen)
ロード後、以下の関数が使えるようになります。
gramschmidt()
ただし、上記のマニュアルを読んでいて気づきました。1行引用させていただきます。
もし xが行列なら、アルゴリズムは xの行に適用されます。 もし xがリストのリストなら、アルゴリズムは部分リストに適用されます。
処理対象のベクトルは行ベクトルか、リストのままの方が簡単みたいです。下手に列ベクトルをガチャンコして行列にしたりすると転置しないとならなくなります。ということで、教科書風の列ベクトル表記を早くもあきらめました。
まずは教科書通りの方法で1個づつ
まずは、リスト形式で基底をなす3個のベクトルを定義しておきます。ついでに前回同様、ベクトルのノルムを計算する関数を定義しておきます。
最初は、ベクトル a1 から 単位ベクトル u1 を求めます。こんな感じ。
次は、求めた u1 とベクトル a2 から u1 と直交するベクトル b2 およびその単位ベクトル u2 を求めます。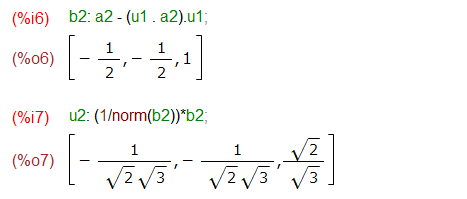
以降、機械的に計算していきます。だんだん計算複雑になりますが、次々とベクトルが求まっていくと。実際に b3、u3の計算が以下です。一瞬、複雑な中間結果に目が回りますが、最後 expand()すれば、あ~ら不思議。
落ち着くところに落ち着いてよかった。ということで u1, u2, u3 への変換できましたデス。
Maximaのgramschmidt関数でやってみる
でも、教科書どおりの方法を「手で」打ち込んでいるのでは段々計算が複雑になると手に負えなくなりそうです。そこで先ほど調べてあった eigen パッケージのgramschmidt()関数を使ってみることにいたします。
使用方法は簡単。eigenロード後、gramschmidt()にベクトル3個をリストの中に並べて渡すだけ。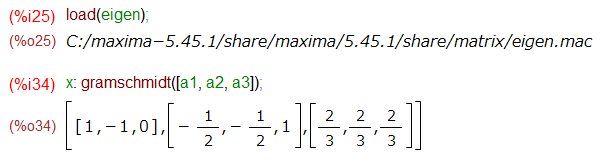
上記の出力は「直交化」なので、先ほどの「順ぐり計算」のb1, b2, b3にあたる「直交」だけれども「単位ベクトルじゃない」ベクトルです。正規化くらい自分でやれよ、と。そこで自前の normailzeL()関数を定義してgramschmidt()の戻り値にmapしてみました。ミソは先ほど使った expand() を入れておいたことです。
順ぐり計算と同じベクトルが得られましたぞ。やっぱこちらの方が楽、とくに空間の次元が増えたりしたら絶対楽。多分。やってないけど。