
前回まで、「対角化」などを「それなりに手順」を踏んで行ってきました。今回のジョルダン標準形への変換はどうしようか迷いました。そのものズバリのJordan行列を扱うパッケージ diag をloadすれば、ほぼ1撃で変換できてしまう。まあ、出来ることをわざわざ刻むことも無し、お楽が一番。手順のみ確認させていただきます。
※「忘却の微分方程式」投稿順 index はこちら
※以下の実習は、みんな大好き Maxima の以下のバージョン(Windows)で行なっております。
-
- wxMaxima 21.05.2
- Maxima 5.45.1 (wxMaximaの裏で動いているMaxima本体)
※以下の参考書の「改訂1」版の演習問題を題材に使わせていただいております。
パッケージ disp のロード
今回は、上記のMaxima環境を立ち上げただけでは初期状態でロードされていないパッケージ disp を使用するので、以下のオマジナイが必要です。パッケージファイルはインストールディレクトリ内に存在するので特にダウンロード等の必要はないと思います。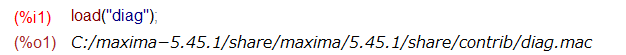
ジョルダン標準形(Jordan Normal Form)への変換
ジョルダン標準形への変換は実質1撃ですが、行列の形で観察しようとするとツーステップとなります。
-
- 関数 jordanに行列を渡すと「リストにエンコードされた」Jordan標準形が返ります。ただしこのリストをみても即座には行列の形は思い浮かびませぬ。
- 上記の「リストにエンコードされた」を受け取る関数がいくつもあり、その中のdispJordanにリストを渡すと、人間可読な行列形式で印字してくれます。
この辺の関数のマニュアル(日本語)は以下に。
上記で得られたジョルダン標準形の検算をするには、変換行列Pが欲しいのですが、上記では見えません。しかしModeMatrix関数に元の行列と「リスト」を渡すとPを求めることができます。
検算できました。
1回では寂しいので繰り返し
型にはめると単純です。別な例が以下に。ちょろい?
A1: matrix([-2, 1],[-1, 0]); L1: jordan(A1) J1: dispJordan(L1) P1: ModeMatrix(A1, L1) P1^^-1 . A1 . P1
上記の実行結果が以下に。
例は人手で計算できる2次でしたが、やっておられるのはMaxima様なので、3次、4次、何次であろうと疲れ知らず。計算はできるけれども、数学の勉強にはならず?

