
前回はアンダーサンプリングでした。今回はCICフィルタです。途中までやりかけて気づきました。僅か2か月ほど前にCICフィルタやってました。年寄りの忘却力は強力。既に頭の中から抜けてました。前回とは目的は違いますがCICはCIC、でも微妙に記号など違っていたので「チョイ直し」でお茶を濁しますです。すみません。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※教科書として読ませていただいておりますのは、三上先生の以下の御本です。
CQ出版社『Armマイコンでつくるダイレクト・サンプリングSDR』
元記事はCQ出版社トラ技誌の2021年連載です。上記はそれをまとめたPDF版のダウンロードサイトへのリンクです。
CICフィルタ、何か月か前にやっていた件
以前にCICフィルタしていたのは、以下の投稿であります。
手習ひデジタル信号処理(41) CICフィルタ使ったデシメータ利用狭帯域フィルタその2
この時はタイトルにありますとおり「狭帯域フィルタ」のためでした。そのときの図やスクリプトが有ったので、今回はそれらをアップデート(チョイ変、手抜きなやつ)です。
まずはブロックダイアグラムです。ほぼほぼ前回同様というか、CICフィルタの1段分はそういうもんだ、と。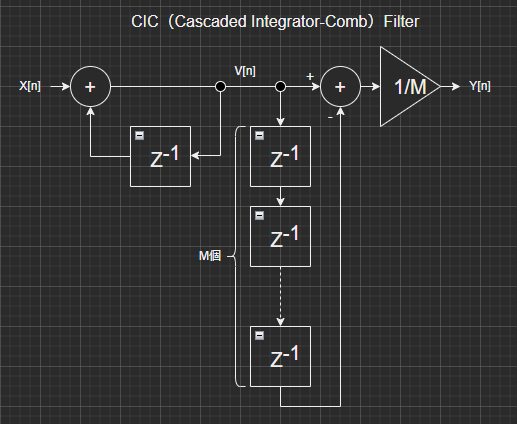
それでも前回は、CICフィルタとしてはありがちな、上記のCICフィルタ1段分を複数段数珠繋ぎに接続していくところの特性を調べていたのです。
でも今回三上先生の教科書では、1段分の特性を勉強することになっていたので、上記を複数段接続するということはありません。そのかわり、以下の伝達関数で、M=5にかぎられていた部分を、いくつか変えて調べることになってます。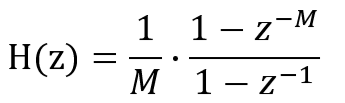
ここまではチョイ直しの中でも「間違い探し」レベルの変更
ゲインプロットするためのScilabプログラム改訂版
さて、本題の振幅特性を計算しプロットするためのコードです。本当は、ScilabでなくOctaveあたりへ移植すれば、両者の「微妙な違い」が分かって良かったような気がしますが、メンドイので、Scilabのままでやりました。
前回は「CICフィルタの数珠繋ぎ」(伝達関数はべき乗となる)だったところを1段に絞ってます、簡単?そのうえ、gainのみ。手抜きだな。
// CIC filter SDR段
clc;
clear();
clf();
M2=2
Hz2 = syslin('d', (1/M2)*(1-%z^(-M2))/(1-%z^-1))
M3=3
Hz3 = syslin('d', ((1/M3)*(1-%z^(-M3))/(1-%z^-1)))
M10=10
Hz10 = syslin('d', ((1/M10)*(1-%z^(-M10))/(1-%z^-1)))
M50=50
Hz50 = syslin('d', ((1/M50)*(1-%z^(-M50))/(1-%z^-1)))
gainplot([Hz2; Hz3; Hz10; Hz50], 0.01, 0.5)
hl=legend(['M=2','M=3','M=10','M=50'],3)
xtitle("CIC Filter M=2~50 正規化周波数 Gain Plot")
プロット結果
三上先生の教科書の「図6 いくつかのMに対応するCICフィルタの周波数特性」というグラフになるべく近づけた結果を得たいと思って Scilabに描いてもらったのが以下です。縦軸、横軸のプロット範囲はほぼ合わせましたが、三上先生の教科書ではX軸がリニアで0はじまり、当方作成版では、X軸も対数で10^-2開始になってます(この辺のScilab制御の仕方が分かってないです。)なお、X軸はサンプリング周波数を1Hzとみたてた「正規化周波数」です。
まあ、Mをデカクすれば高い周波数のゲインが低下し、通過帯域が狭くなるという結論は「見えている」ようなのでOKっと。
いつにも増して手抜きだな。自分。だいたい今度こそ、忘却力に対抗できるのか?
