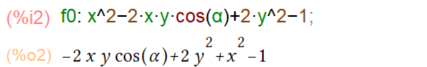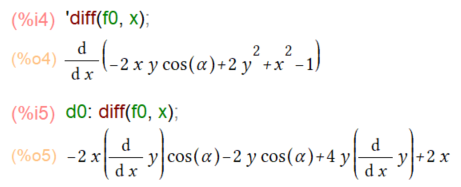前回までダラダラと微分の練習。Maxima様にお願いすれば微分自体は一撃。しかしメンドイのはいつも後始末です。今回は、前回までと異なり変数間の関係がそのままではわからない陰関数の微分です。今回も微分そのものは一撃。しかし事前にひと手間かけないとならなかったです。いつもの通りの後始末もメンドイ（計算してもらってるのに。）
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の問題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
※参照させていただいている Maximaのマニュアルページ（日本語）は以下です。
陰関数の微分
前回までやってきた「あからさまに関数の形をしている」陽関数の微分と比べると、「陰関数」の微分はひと手間かけないとなりません。どの変数がどの変数の関数なんだかMaxima様にお知らせせねば微分できないっと。
それさえできれば微分は一撃ですが、例によって微分の後の後始末も多少メンドイです。
でもま、今回の処理を並べればこんだけ。
f0: x^2-2*x*y*cos(α)+2*y^2-1; depends(y,x); 'diff(f0, x); d0: diff(f0, x); solve(d0, diff(y,x));
まずは陰関数の形から。こんな形。
さて今回の例題の左辺部分を書くと以下のようです。
ただ、このままではyがxの変数だということはMaxima様には伝わりませぬ。人間的には見ればわかるだろ～というお約束ですが。
そこで、yはxの関数なのよ（依存しているのよ）とお伝えする。
そして、f0をxで微分するところは、以下のように一撃（上の行で、ことさらに微分する前の式を表示してたりしますが。）
しかしな～、上の微分結果、人間的には納得いかねえずら。やっぱり、dy/dx=なんたら、という形になってないと。
そこで上記の結果をsolveに渡して「方程式の求解」してもらいます。この微分後の整理のパターンは今までの陽関数の微分のときとはチト違うね。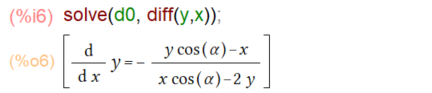
求まりました。これならＯＫかね。多分。