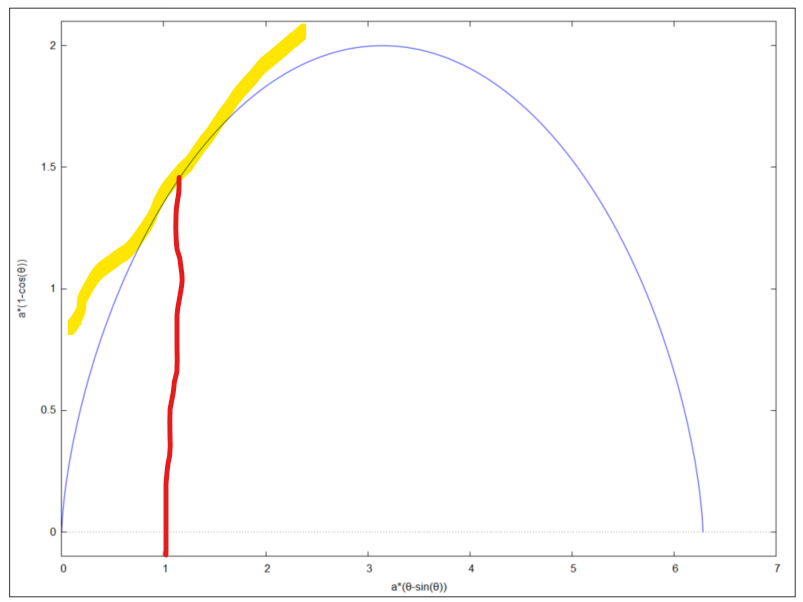
今回は「媒介変数」表示のサイクロイド曲線を微分し、接点での勾配を求めて接線の方程式を求めよ、と。アイキャッチ画像に汚く書き入れましたが、赤の位置で黄色い接線の方程式を求めます。前回までのように diff()は一発、後始末すればOKというパターンからはちょいと面倒。やってみればなんとかなりそうな、そうでないような。。。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回気づいたのですが、Parametricプロットの引数の並べ方、昔のMaximaとはちと違うような気がします。といって古い版がないので確かめようもないのですが。
サイクロイド曲線
媒介変数Θをつかって表現したXとYの位置が曲線を与えます。車輪に見立てると a は直径ってことですかい?知らんけど。
wxMaximaなので、wxplot2d(本体ではplot2d)で「半回転分」プロットしてみます。こんな感じ(なお直径aは1という設定デス。)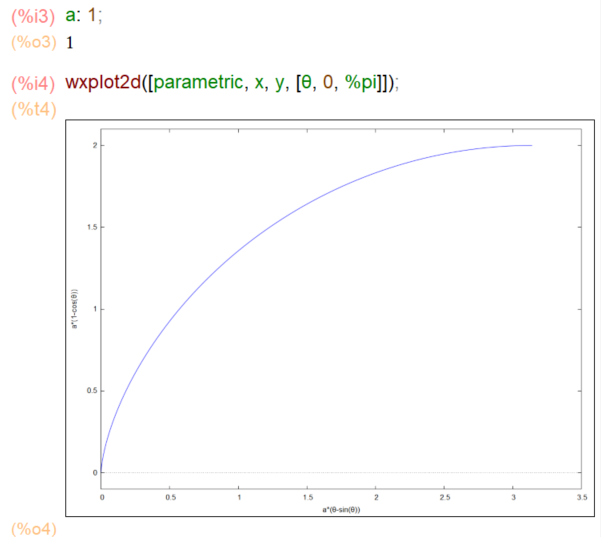
サイクロイド曲線の微分
さて、上記のyはxの関数なので、yはxで微分できるハズ。微分するにあたっては、以下の公式そのままでやってみました。もっとかっこいい方法あるのか、ないのか?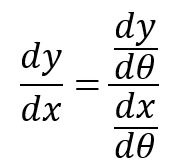
dy/dΘをYD、dx/dΘをYDとして計算してみたものが以下に。
dy/dxを求めると、上記のように a は消えてしまいます(直径に関係なく、車輪の回転、当たり前か)
接線の式を求める
微分できたので、Θに特定の値を代入すればその位置での勾配が求まります。例題では Θ=π/3 での接線を求めよ、ということであったので代入。
勾配が求まりました。
Θ=π/3 での x, y座標(接点)を求めると以下のようです。
勾配と接点位置が求まったので、接線の方程式は以下だと(変数はY,Xとしています。%o18は勾配、XY[1]が接点のX座標、XY[2]が接点のY座標です。)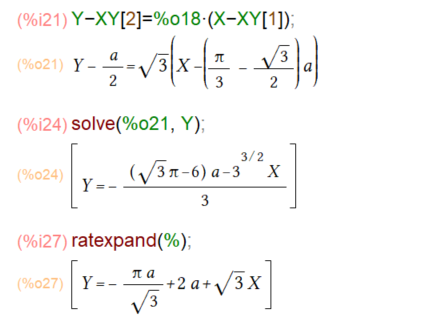
結果を整理するのに、solveしてratexpandしてますが、なんとか「人間可読な感じ」のお答えが出ました。チョロイようなメンドイような。