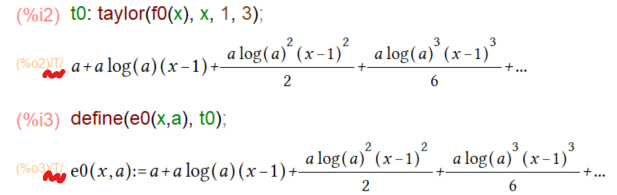今回はテイラー展開。高次微分ができる関数ならば多項式で近似できるアレ。わずか3か月前にテイラー展開の特殊な場合であるマクローリン展開する必要があり、やってました。しかし老人の忘却力です。すでに肝心なところを忘れておりました。マクローリン展開のときに引っかかった同じところに、再び引っかかると。学ばない人、いや忘れる人か。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔、大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
テイラー展開
数か月前に、マクローリン展開する必要があってやったときの投稿が以下に。御存じのとおり、マクローリン展開は「原点付近」でのテイラー展開なので、このときも使ったMaxima関数は Taylorでした。
忘却の微分方程式(53) 唐突にマクローリン展開して limit、Maxima
テイラー展開についてのMaximaマニュアル(日本語)は以下に。
28. Sums, Products, and Series
テイラー展開、例題その1
taylor展開したところが以下に。微分さえできればテイラー展開は簡単に求まります。赤の波線つけた /T/ は上のマクローリン展開のときに調べました。CRE(標準有理式)という再帰的な表現のうち、テイラー級数の表現用の拡張CREのシンボルなんだそうな。知らんけど。
上記では、3次まで求めたテイラー級数をつかって関数の値を「数値」として評価するために、関数定義してます、defineで。しかし、実はここでハマってました。
:= で関数定義すると、テイラー級数を数値で評価できませぬ。
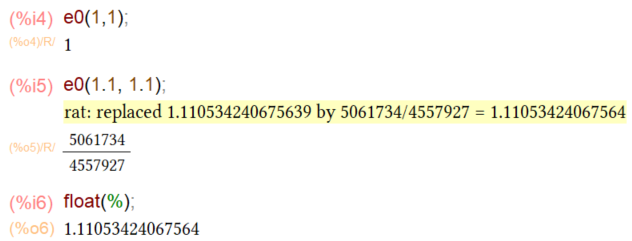
なぜだ~といってもMaxima素人にはその理由は定かでありません。しかしこれはマクローリン展開したときにすでに経験してました。忘れてた。define関数使って定義すれば、数値で評価できます。ほれこのように。
上記のようにテイラー級数そのままで関数定義すると結果を「分数」で表現してくれるようです。浮動小数点数でほしければ、float()する必要がありました。「1.1の1.1乗」を関数電卓で計算した結果は
1.1105342410545757282895080395066
でした。まあ、3次でもいいんじゃないかい。いい加減な。
テイラー展開、例題その2
つづいてもう一つ。上記例で経験したので、taylor展開後の評価用の関数定義は最初からfloat()でくるんでみました。するとtaylor展開の係数もfloat化されるのね。あたりまえか。なお、x=0付近での展開なのでこれはマクローリン展開でもあります。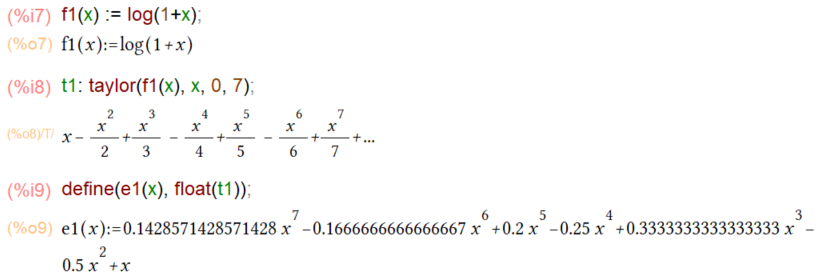
上記の7次までの級数で計算してみた結果が以下に。関数電卓の数字は以下です。0.09531017980432486004395212328077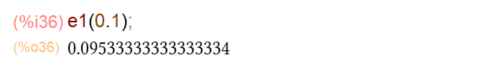
0付近での展開なので、上記の0.1あたりではそれっぽい値ですけど、ちょっと1離れるだけでハシボーでした。こんな感じ。
実際に近似計算するときは、テイラー展開よりずっと収束の早いアルゴリズムがあるのだろうけど、多分。