
前回は置換積分法をつかってなんとか積分。今回は教科書の部分積分法の例題。こちらは部分積分など考えずとも integrate 一発で積分可能。しかし事前の assume 必要デス。いままで assume は「>」とかばかりでしたが、「xxじゃない」not equal はどう書いたらよかったんだっけ?「!=」じゃないし。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
大昔大学生のときにこういう御本が欲しかったです。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
簡単に解けてしまう奴ら
部分積分のところから定積分の例題をいくつか使わせていただいたのですが、簡単な奴らは一撃でMaxima先生は解いておしまいです。こんな感じ。
もういっちょも、こんな感じ。
ううむ、このままでは今回盛り上がりに欠けるな、と。勝手な感想。自分じゃ計算してないからお気楽なものです。
条件が必要な奴ら
以下は不定積分ですが、「nは-1でない」との条件がついてます。何もせずに integrateしてしまうと以下のように Maxima先生から条件の尋問を受けることになります。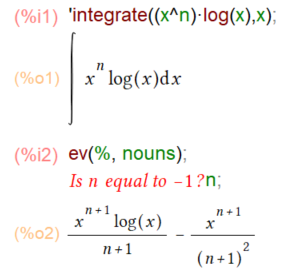
まあ、インタラクティブに n とか否定すれば所望の結果(未整理だけれども)に到達できます。
念のため、-1 だったときどうなるのという側も計算していただきました。こんな感じ。
結果、あっているのか? 知らんけど。
さていちいちインタラクティブにMaxima先生にお答えするのは骨がおれます、というよりバッチ実行のときにはマズかろうと。そこで事前に assume してみるかと思ったのです。過去の assume は、
a > 0
みたいな不等号つかった表現ばかりでした。今回は -1 でないということです。C言語頭で考えると a != 0 ですが、これはMaxima先生の受け入れるところではないようです。not equal は notequal()だと。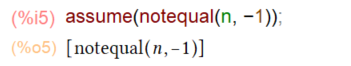
上記のように assume しておけば、以下の不定積分は順調です。
最後、factorで結果を「おまとめ」してみました。
さてもう一題、assume(notequal( が必要なお題デス。
できました。なんだassume簡単じゃん。ホントか?
