前回は地震の震源?を3次元空間にプロットしたらばプレート界面らしきものが浮かび上がってきました。今回は乱数を3次元空間にプロットすると平面が現れてくるの巻です。最近使われるカッコイい乱数発生アルゴリズムではなく古典的な線形合同法によるものです。VAX FortranのRANDU関数とな。ナツカシー?
※「データのお砂場」投稿順Indexはこちら
今回のサンプルデータセット
今回の randu というサンプルデータセットの解説ページは以下です。
Random Numbers from Congruential Generator RANDU
この解説ページを読んで懐かしいお名前を目にしましたぜ。VAXとVMSです。今時の若者は知りますまい。VAX-11は、解体され買収されて姿を消したDEC(Digital Equipment Corp.)のベストセラー32bitミニコンです。16ビット世界のスタンダードPDP-11を32bit化するとともに仮想記憶化したもの。1980年代前半、まだマイクロプロセッサが64Kバイトのメモリ空間のくびきに喘いでいたころ、世界で一番勢いのあったコンピュータじゃないかと思います。そしてVMSはそのオペレーティングシステムです。わたしゃVMSにお世話になっていたので、VAX用のUnixが登場したときに「何、このおもちゃみたいなOS」などと悪態をついていましたぜ、すみません。
さてデータは、VMSオペレーディングシステム上のVAX FORTRANコンパイラに実装されていたらしい乱数生成関数RANDUの生成した乱数列です。すみません、VAX FORTRAN、使ったことないです。でもま、その当時には結構使われていた筈。ただ、当時は乱数発生器の実装はまだまだ未熟?で線形合同法だったみたいです。簡単だしねえ。
まずは生データ
x、y、zという3つの列に分かれていますが、400行3列の乱数データのようです。データの素性を観察するために summaryとった結果はこちら。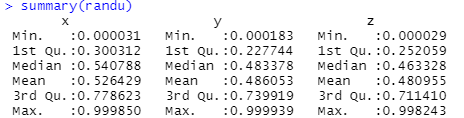
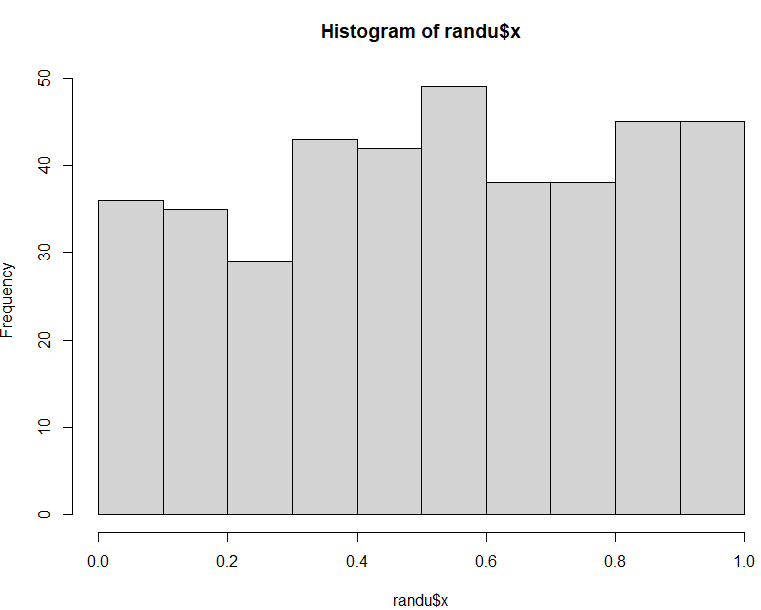
0から1の間の乱数みたいっす。その分布を確かめるためにヒストグラムも描いてみました。操作はこんな感じ。
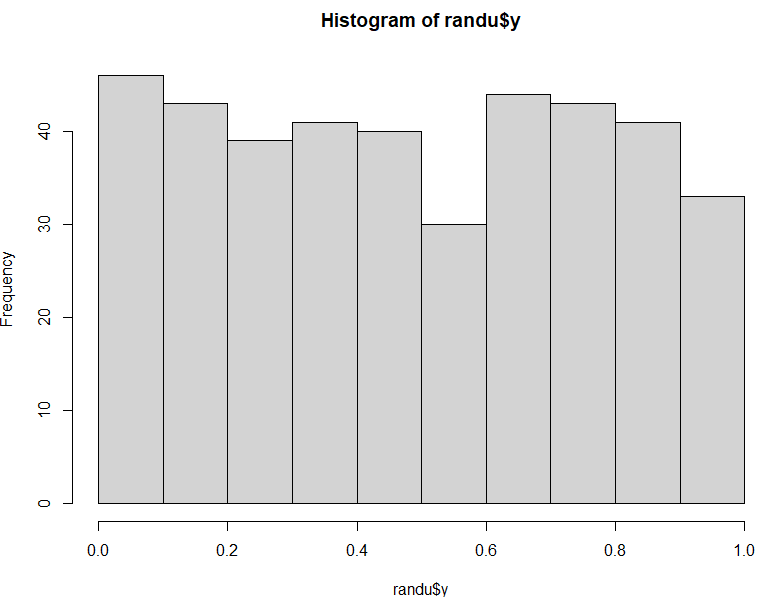
Y列のプロット結果
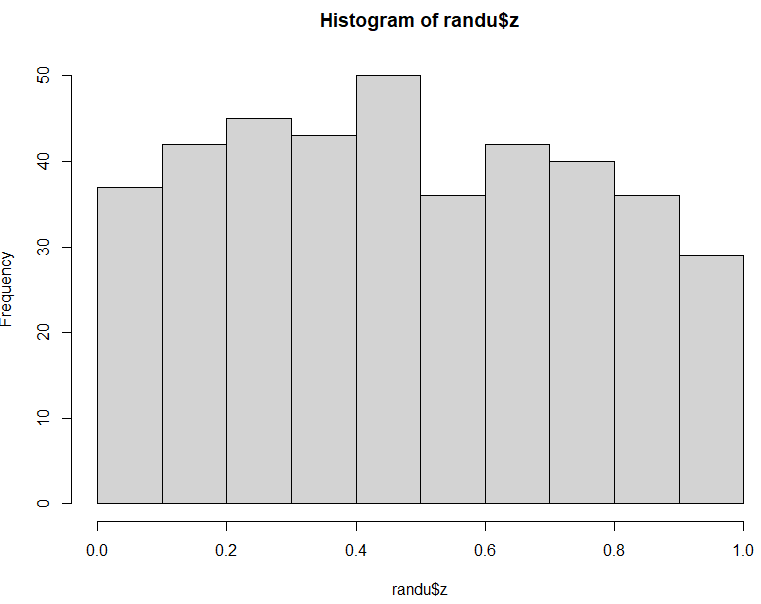
Z列のプロット結果
データ点数が400点なので多少凸凹があるけれども、まあ一様乱数?なんではないかと。
先に処理例を動かしてみる
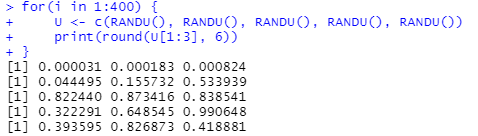
解説ページには処理例が掲載されていますが、今回の処理例はサンプルデータセットを処理するものではなくて、サンプルデータセットを「生成」する側のもの。VAX FORTRANのRANDU関数相当のR関数は以下のように定義できるみたいです。簡単?
長いのので以下は省略であります。
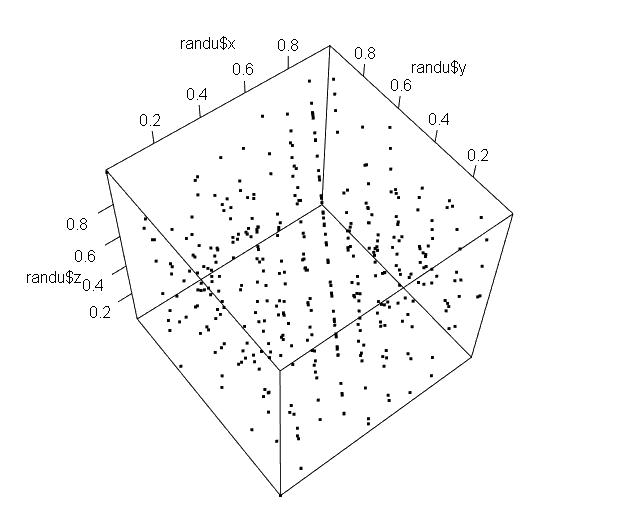
線形合同法の欠点、「乱数は平面に落ちる」をプロット
サンプルデータが固定間隔でとりだした乱数3個の組x、y、zであることからして、その意図は3次元空間にプロットすると乱数が平面に乗ってくることを示したいのだと想像しました。その辺の乱数の事情を説明するよさげな資料を探していた以下を拝見いたしましたです。広島大松本様、
上記のP.11に「乱数が平面に落ちる」プロットが掲載されています。あざーす。点数が多いのでよい感じです。
サンプルデータは400点なのでイマイチですが、以下のようにすれば眺めることができます。
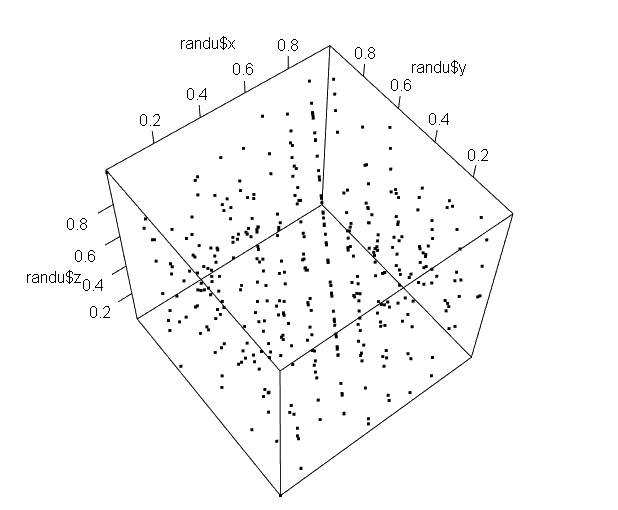
実際のプロットが以下に
斜めの角度になると分かりずらいですが、並行な平面上に点がならんどります。たしかに「平面に落ちて」ます。
「天網恢恢疎にして漏らさず」どころかダダ洩れであると。ホントだ。まあ最近では組み込みマイコンでもTRG(真性乱数発生器)登載しておるものなあ、線形合同法は使わんよなあ。