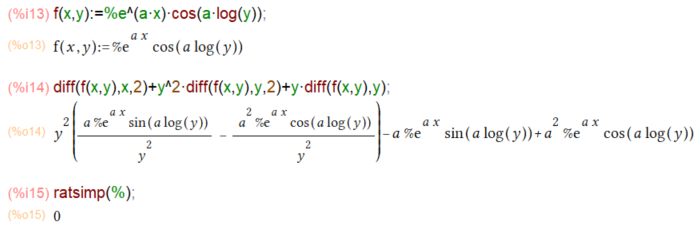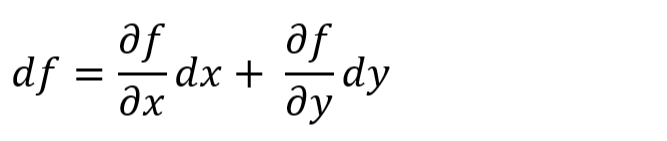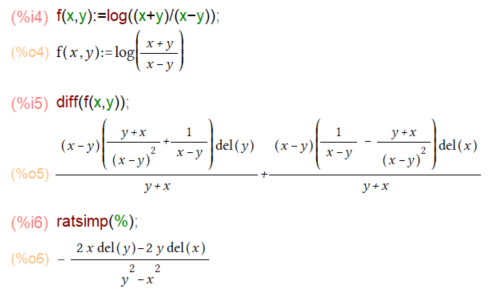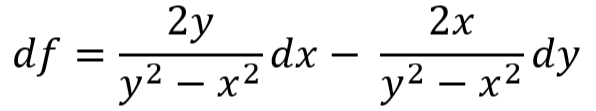チンタラMaximaの練習していたのでは「死ぬまでに読みたい」御本が読めないなと鉢巻を締め直しました。御本はみな工学書にて数学科の数学みたいなムツカシーものは出てきませんが、数学不得意な上に寄る年波で計算ができない年寄には過ぎたる数式多数。そこをMaxima様にお願いしたいとの希望あり。ピッチを上げろと。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
※いつもお世話になっておりますMaximaの日本語マニュアルのうち、今回参照させていただきます微分関係のページは以下です。
残念な点これあり
今回は偏微分、全微分がテーマですが、こいつら解くためのMaximaの関数は既に何度も練習してきた diff()です。いままで通り。使い方は分かっている（ホントか？）ということで嬉しいのですが、残念なことが一つあります。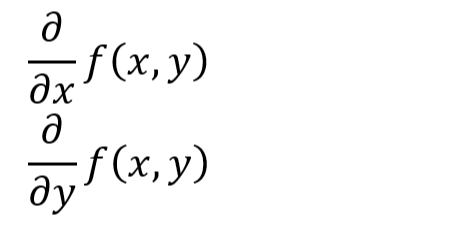
偏微分の時にお世話になる「∂（ラウンド）」記号を画面出力する方法が見当たらぬことです。積分などは「名詞形」で評価を止めてやれば積分記号が画面出力されるのに。また、dx, dy などと書いたら人間はこれが微分の意味だと理解しますが、Maxima様はそうではありませぬ。人間的には dx, dy と表現するところを
del(x), del(y)
などと表現してくれます。イマイチ分かりずらいっす。一段と人間の目に分かりやすい表現は数式エディタにお任せしないとならないようです。
まずは偏微分
ということでまずは偏微分。以下のf(x,y)をxとyでそれぞれ偏微分してみます。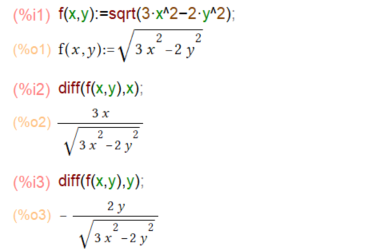
今までも微分はdiff(f(x), x) などとしてきたので何も変わりませぬ。一撃。
それどころか高次の偏微分も同じくできまする。以下のf(x,y)に対して、２階の偏導関数を含む下の式の値を求めよと。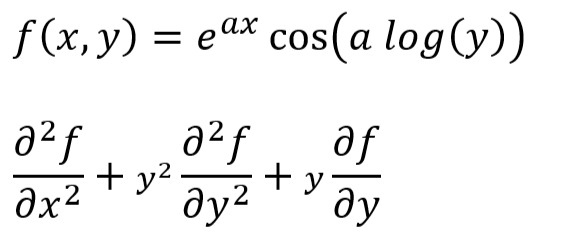
Maxima様にお願いすれば、ほれこのとおり。
一瞬目が回りそうな式が出てまいりましたが、ratsimp()一発で最短の結果に落ち着きました。よかった。
全微分も出来たのね
教科書に出てくる全微分は以下のようですが、
実はdiff()関数は全微分も求めることができるのでした。今までｘで微分するからdiff(f(x,y), x)などと変数を指定してきましたが、「全」微分なので、ｘとかｙとか、つべこべ変数指定しなければよかったのです。
例題はこんな感じ。
これまた全微分の直後は長い式がボロリンですが、ratsimp()が整理してくれます。ただ、さきほど出てきたdel(x), del(y)表現が出てきてイマイチ目に優しくありませぬ。
ここの清書のみ自分で行いましたです。
いい感じに全微分もできてるじゃん。