前回は三重積分でしたが、今回は2重積分に戻ります。平面座標系(x,y)から極座標系(r, θ)に変換した方がよろしいんでないかい、という極座標への変換を行うケースです。あれれ、2変数のときの変数変換ってどうやったら良かったんだっけ?ヤコビアン?めんどくせーお名前の奴が召喚されてきました。どちら様でしたっけ?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
極座標への変数変換
ヤコビアンについて数学素人が知りもしないことを書き連ねてもせんないので、いつもお世話になっております「高校数学の美しい物語」様の以下の記事などご覧になってくだせーまし。
以下に変数x, yで定義された二重積分を変数u, vでの二重積分に変換する場合の公式を掲げました。ヤコビアンJが >0 ならば以下のようです。でもメンドクセー。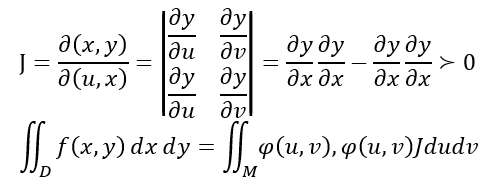
上記を平面座標(x,y)から極座標(r, θ)での二重積分に変換する場合に限れば、x=r*cosθ、y=r*sinθであるお陰を持ちまして以下のようにスッキリ?っす。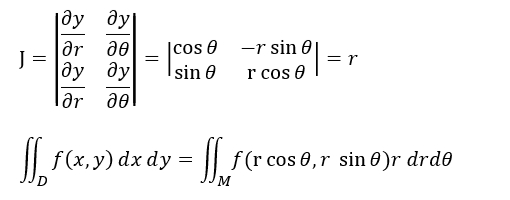
なんだ、極座標変換のときは、ヤコビアンって r になってしまうのね。
今回の例題
上記をみると、結局積分領域DからMへの変換こそがキモって感じがしないでもないです。さて今回の例題はこんな感じ。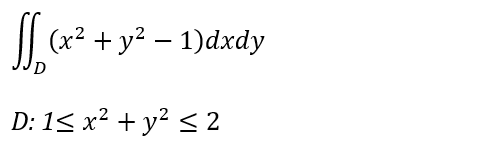
極座標への変数変換のページの例題なので、いかにもそれらしい積分領域Dの例題です。例によってMaxima様で、Dのプロットをすべしと考えましたが、これが結構マニアックでした。これまた、いつもお世話になっておりますMaximaの日本語マニュアルの以下のページに region の使い方書いてあります。なんと、上記のDのような不等式を and したり or した領域を塗りつぶせます。いいことが分かったな。今後の塗りつぶしはこれだね。
プロットに使用した入力行が以下に。
draw2d(x_voxel=100, y_voxel=100, region(x^2+y^2<=2 and x^2+y^2>=1, x, -2, 2,y, -2, 2))
プロット結果が以下に。まん丸のドーナツ型であります(縦y、横x)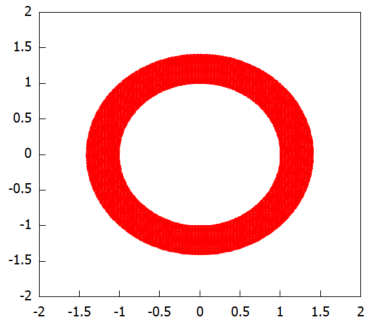
ドーナツ型は目出度いです。まさに極座標変換してくれ、という形。極座標変換した後の積分領域Mをプロットしてみます。プロットに使用した入力行が以下に。
draw2d(fill_color=green, filled_func=sqrt(2), explicit(1, θ, 0, 2*%pi), yrange= [0, 2]);
のっぺりした長方形になりました。こうなればこっちのもんだね。
極座標変換した二重積分式をまずはシングルクウォートの「スンドメ」モードで 入力してみました。
そして、ev()関数で評価すればお答えが出ましたな。ま、極座標変換したところで既に答えはみえておったと。ホントか?