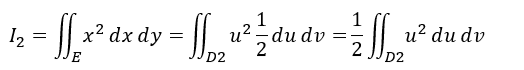前回まで極座標変数変換を行って二重積分を解く例題をやってきました。今回も最終的には極座標変数変換で解くのですが、1回ではできず変数変換を2回やる「合わせ技」のスタイルです。積分領域は都度グラフ化して確かめてみます。当然ヤコビアンさんも登場。今回はMaxima上でヤコビアン(行列式)を求めるのも練習してみます。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題は2ステップ
以下が今回の例題です。見れば分かる通りで2重積分自体は同じなのですが、積分領域がDとEと異なる2題です。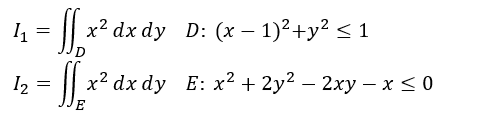
意図が透けて見える気がするのは、積分領域がやや単純にみえるI1の結果がきっとI2を求めるときに役に立つのだろう、と。知らんけど。
まずはI1の積分領域Dをグラフ化
前回、前々回とやってきたように、draw2dの引数にregionで領域を指定する「技」大変便利です。今回もDの描画は以下で一発。
draw2d(x_voxel=100, y_voxel=100, grid=true, proportional_axes = xy, region((x-1)^2+y^2<=1, x, -0.5, 2.5, y, -1.5, 1.5))
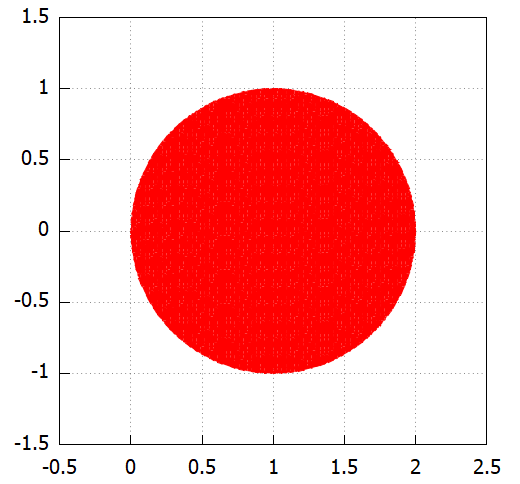
領域Dのグラフ化の結果が以下に。日の丸的な。
なお、x_voxel=100とか指定しなくても描画はできますが、結構カクカクします。
上記をみれば、極座標変換 x=r*cosθ、y=r*sinθ を行ったときに元の積分領域
D: (x-1)^2+y^2≦1
が、新たな積分領域Mで以下のようにかけるのは納得いきます。
M: 0≦r≦2cosθ, -π/2≦θ≦π/2
数学不得意の年寄はグラフ描いてようやくわかった気がすると。ホントに分かったのか。
I1の積分
既に前々回やったとおりで、上記のような極座標変換のときのヤコビアンさん(行列式)Jは
J=r
と分かっているので、変数変換後の積分は以下のようにかけます(積分直前で止めておくスンドメ・スタイル)
I1: 'integrate('integrate((r*cos(θ))^2*r, r, 0, 2*cos(θ)), θ, -%pi/2, %pi/2)
実際にMaxima様に積分をお願いしたところが以下に。
ここまでは前々回の範囲の復習っと。
さてI2の積分範囲Eをグラフ化
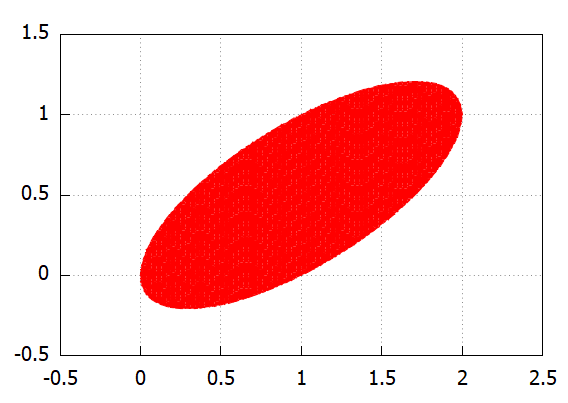
見れば分かる円の形であった積分領域Dと比べるとI2の方の積分範囲Eはチョッチ複雑っす。数学不得意の年寄は思い描くことができませぬ。しかし、draw2d+regionは最強コンビです。お願いすれば、これまた一撃。
draw2d(x_voxel=100, y_voxel=100, grid=true, proportional_axes = xy, region(x^2+2*y^2-2*x*y-x<=0, x, -0.5, 2.5, y, -0.5, 1.5))
前回、楕円をやりましたが、今回のは長軸、短軸がひねくれて?いるやつ。こういうときはどしたらよいの?
I2最初の変数変換
上記のグラフを見ても数学不得意の年寄にはどうしたら良いのか具体的なアイディアなど湧いてきませぬ。ただ、上記の捻くれた楕円も何か変数変換したらば「きっと最初の円」に移し替えることができるのであろうと勝手に想像。教科書に曰く(見てしまったのね。。。)
x=u, 2y-x=v
とu, v に変数変換すれば 領域Eは以下のようになると。あれまDと同じ形。
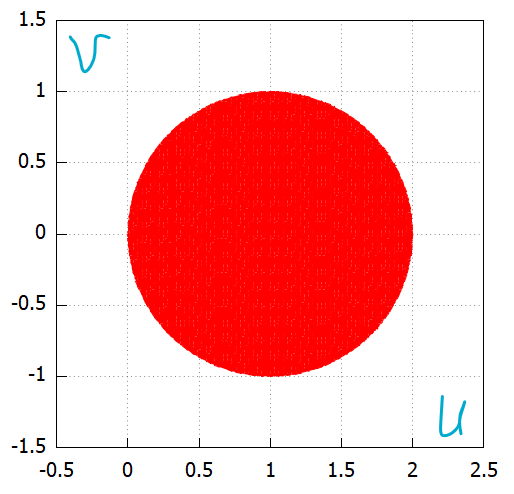
D2: (u-1)^2+v^2≦1
I1の時と同じ、日の丸弁当。ただし、横軸 u の 縦軸 v です。変数変換しているので、このu, v 変換(x=u, y=(1/2)*u+(1/2)*v)のときのヤコビアンさんを求めなければなりません。
Maxima様にもヤコビアンさんを求める関数あり、ドキュメントは以下に。
上記に Jacobi行列を返す jacobian(f, x) が説明されております。ただしjacobian()関数はヤコビ「行列」を返してくれるところまでで「行列式」ではありませぬ。そこで以下のようにして今回必要なヤコビアンさんJ(行列式)を求めました。
綺麗で後が楽そうな結果が求まってとても嬉しいです。
I2の積分を求める
上記の変数変換によって、以下のようにI1の結果に、上で求めたヤコビアンさんを乗じてやればI2のお答えとなることが分かりました。
Maxima様にお願いするほどの計算でもないですが、お願い。
求まってしまいました。ヤコビアンさんを計算できれば1撃だったと。