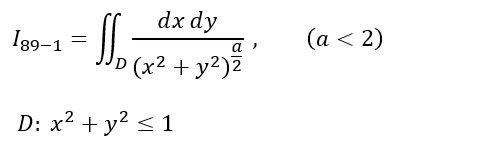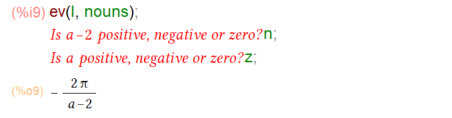前回は3重積分だったですが、今回は何度目かの二重積分です。しかし「特異点」登場。Singularityってやつ。恐ろし気な。。。無限大が出てくるのに定積分が計算できてしまうとはこれいかに。数学素人の年寄は目が回るばかりですが、数学じゃ「あるある」。そういえばいつもお世話になっているフーリエ変換様も区間無限大か。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
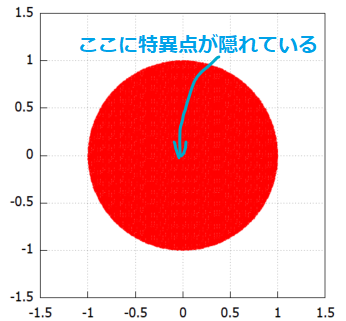
今回の例題は以下の通りデス。特異点どこ?
定数 a が正(ただし a<2と条件ついているので 0<a<2)のときに、分母の方をみていただいくと、原点(0,0)が目出度く特異点になっております。
数学素人が広義積分について語ってもせんないので、いつもお世話になっております『高校数学の美しい物語』様の以下のページのURLを貼り付けさせていただきました。
そうだね~やたら無限大∞まで積分ってパターン多いよな。これ無には工学など何もできへんという感じ。広義積分にはいつもお世話になっておるのだな。あざーす。
積分領域Dをグラフに
例によってまずは積分領域Dをグラフ化してみます。Maxima様にお願いする方法は以下の通り。
draw2d(x_voxel=100, y_voxel=100, grid=true, proportional_axes = xy, region(x^2+y^2<=1, x, -1.5, 1.5, y, -1.5, 1.5))
いつもの通りで「日の丸」プロットを描けました。しかし今回は、このDの真ん中(0,0)のところに特異点が隠れているのであります。
まあ、X、Y座標のままだと領域の真ん中にブラックホールかのごとく特異点があることになってしまうのでメンドそうです。当然、ここ数回学んだとおり、極座標に変換かと。
極座標変換とヤコビアンさん
まずは極座標変換の座標変換を書き表し、例によってヤコビアンさんを計算しておきます。すでに2次元の極座標変換するときのヤコビアンさんの値は何度もやって分かってますが、ことさらに計算してます。
X: r*cos(θ) Y: r*sin(θ) J0: jacobian([X, Y], [r, θ]) J: trigrat(determinant(J0))
上記の結果がこんな感じ。ヤコビアンさんが召喚されました。
さて積分
積分領域Dは、以下のように極座標変換によってMに写ってます。
M: 0≦r≦1, 0≦θ≦2π
ヤコビアンさんが召喚されていれば、積分を書き表すのは簡単。
F: 1/(X^2+Y^2)^(a/2)
I: 'integrate('integrate(F*J, r, 0, 1), θ, 0, 2*%pi)
今回は、aの値によってどうなるのか慎重に、といってMaxima様に丸投げで計算していただきました。まずは、無難な aが負のとき。
結果もとまったようです。続いてaが0のとき。
これまた求まりました。aが0だって言っているのにこれ以上は勝手に簡単にしてくれたりしないのね。
なんだ、求まるじゃん。特異点をすり抜け(ちょろまかし)た?