
3次元空間の領域Dを3重積分すれば体積が求まると、道理であります。積分領域Dが簡単ならば何も言うことはありませぬ。しかし、ちょいと捻くれたDを相手にするとへなへなと萎れます。どしたら良いの?そういうときこそヤコビアンさんの出番かもしれませぬ。今回は上手く行くケース、例題だから当然っちゃ当然。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回の例題
まずは、x, y, zの3次元空間の中の領域Dを3重積分するならば体積Vが求まるという、「道理」な式を上に掲げまする。そして、今回の例題で求めるべき領域Dの定義が下に。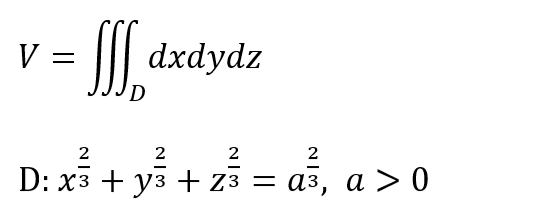
積分の中身は簡単だけれども、領域がメンドイっす。3分の2乗って何よ、なんだかな~な感じだね。
積分領域Dを図示
凡人はグラフでも目にせねば、Dのイメージが湧きませぬ。式の形からして原点対称な図形みたいだけれども。
例によって定数 a に何か値を与えねば具体的にグラフにできんので 1 としてみました。グラフを描く操作が以下に。
a: 1; D: x^(2/3)+y^(2/3)+z^(2/3)-a^(2/3); draw3d(implicit(D, x, -1.5, 1.5, y, -1.5, 1.5, z, -1.5, 1.5));
描いたグラフが以下に。何やら、忍者のマキビシみたいな形です。これを積分せよというのか、メンドそう。。。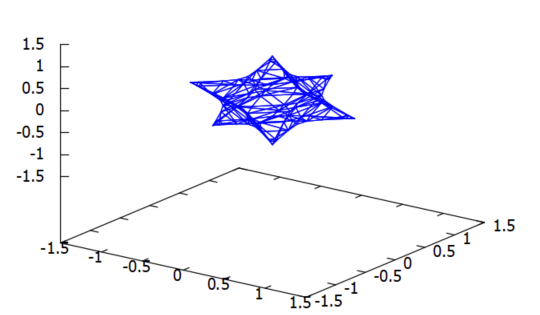
変数変換
グラフの形から、これは例によっての、極座標変換だな~と想像したのですが、教科書では直接極座標変換ではなくて、ヤバそうな3分の2乗のところをまず変数変換してました。
-
- 第1ステップ
以下のような新たな変数X, Y, Zを導入することで、x^(2/3)は、X^2のようなスッキリした形にできると。ついでにヤコビアンさんを求めると以下のようです。
つづいて、本命の空間極座標(r, θ, φ)へと変換。
-
- 第2ステップ(空間極座標変換)
先ほどの、X、Y、Zをr, θ, φで書き直し、再びヤコビアンさんを求めます。
trigratでスッキリ。
3重積分
さて、上記2段階の変数変換により、積分すべきものは、ヤコビアンさん2つを乗じたものとなりました。さらに極座標化した積分領域を、「赤道」で割って、さらに緯度方向で4分割して8つに分けたリンゴ風にしてみると、8分の1部分の積分I8は以下のようになるとです。
なお、ヤコビアンさんの1つめ J0bは、X、Y、Zを(r, θ, φ)で書き直す前に求めているので、ev()にかけてX、Y、Zをr, θ, φに直してから乗じてます。
I8は8分割した切れ端なので、最後お答えを求めるところで8倍して全球形状にしとります。なお、ずっと前の方で、a=A^3とおいていたので、忘れずに元の aに戻さねばなりません。上記では忘れていたので手書きです。なんだかな、ヤコビアンを求めるたびにDがやせ細ってJの方に移っていく感じ。。。ヤコビアンさん流石。