前回は体積、今回は表面積デス。今回は高校生の皆さまならば一瞬で解ける部分にハマりました。入試なら落ちてマス。教科書は「楕円の一般形」の式に帰着させるのに「平方完成」していたのです。そこに踏み込んだ忘却力の年寄は難渋しました。しかしMaxima様にお願いするならそんなテクなど無用、そのまま計算すれば良かったのです。即答。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
曲面積を求める公式
今回使用する曲面積を求める公式は以下です。
２重積分の中に偏微分が入っていてメンドクセー感じもしますが、素性は悪くないです。ぶちゃけ、偏微分の素性が良ければ、現れてくる以下の２重積分は領域Dの面積でしかありません。Dが「求まれば」実際には２重積分することもないっと。
今回の例題
今回の例題を図時してしまいます。
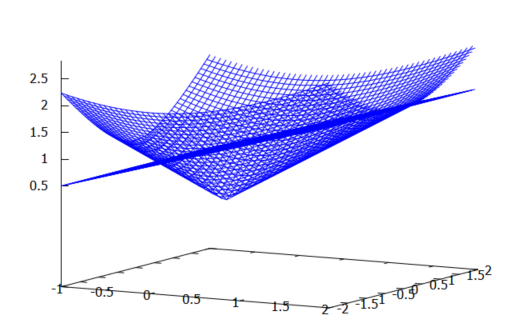
上記のグラフ描画をMaxima様にお願いするコマンド列
が以下に
F(x, y)が直円錐面を表しており、G(x,y)はそれに交差している平面です。
-
- 直円錐面が平面から切り取る面積S1
- 平面の下方にある直円錐面の曲面積S2
を求めよ、とうのが今回の例題っす。
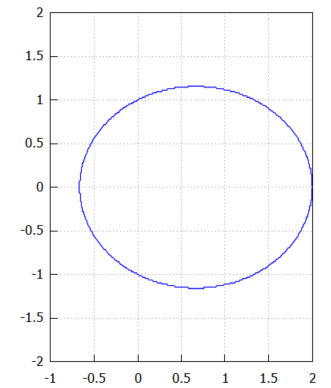
そこでクローズアップされるのが、平面と直円錐面の交線をxy平面に正射影した２次元図形Dです。これが積分領域となるっと。こちらをグラフ化してみるのには以下のように。
描いた図形が以下に。楕円ですな。
楕円の一般形を求めるのにハマる
教科書では、Dの面積を求めるのにF(x,y)とG(x,y)の交線の式を「平方完成」して「楕円の一般形」に持ち込んでいるのです。そうすれば 面積は πab っと一撃。
教科書は大学初年級くらい向けだと思うので、まだ受験勉強の記憶もフレッシュな方々相手なのでしょう。「楕円の一般形」、「平方完成」なんかお茶の子サイサイだという想定だと思います。実際、受験勉強向け？の以下のサイト様に懇切な解説記事を見つけました。あざーす。
トライ様 5分でわかる！楕円の一般形
進研ゼミ様 【２次関数】平方完成の手順について
高校生の皆さまなら一撃、の上記作業にかなり時間つかってしまいました。忘れとる上に、手作業で解こうとしてダメダメでした。
結局、T0=0の式を、E0のような標準形にするのに、かなり苦しんでa, b, p, q を決めました。楕円の面積はSe1（「有理化」して8√3*π/3)であります。これが求まれば後でみるとおり曲面の面積など一撃です。しかし、Maxima様にお願いするのであれば、わざわざ標準形にする必要などありませんした。
何も気にせず２重積分してしまう
Maxima様にお願いするのなら、「楕円と見ぬいて」わざわざ標準形に帰着させるなどという「知恵」を使わずとも、y=の形にしてそのまま積分すれば楕円の面積が求まります（楕円かどうかなど気にしないケド。）
それどころか、上記のように領域Dの面積を別途求めるなどしなくても、直に公式を適用してS1、S2を計算する方がお楽。なお、以下ではx軸より上半分のみ計算して最後で２倍してます。まずはS1。
続いてS2。
式が複雑になったって計算はMaxima様じゃ。そのまま計算するのがお楽。