大分以前にAnalog Discovery2からのデータの「輸出」をやってみました。しかしCSVファイルに書き出しただけで終わってました。そこで今回は別シリーズ「手習ひデジタル信号処理」で活躍中のScilabでAD2のデータを読み込んで解析らしきことを試みてみます。読み込んでしまえばコッチのもんだと。ホントか?
※「お手軽ツールで今更学ぶアナログ」投稿順 indexはこちら
今回「輸出」する信号
今回「サンプル輸出」する信号は以下の別件記事で取得した「だいたい」正弦波な信号です。
定番回路のたしなみ(39) MOSFET、ソースフォロワ回路でアナログ・レベルシフト
黄色C1がオフセット0V、振幅500mV、周波数1kHzの入力信号で、青色C2がオフセットが約1.28Vに持ち上がった出力信号デス。AD2の制御ソフトであるWaveFormsの画面はこんな感じ。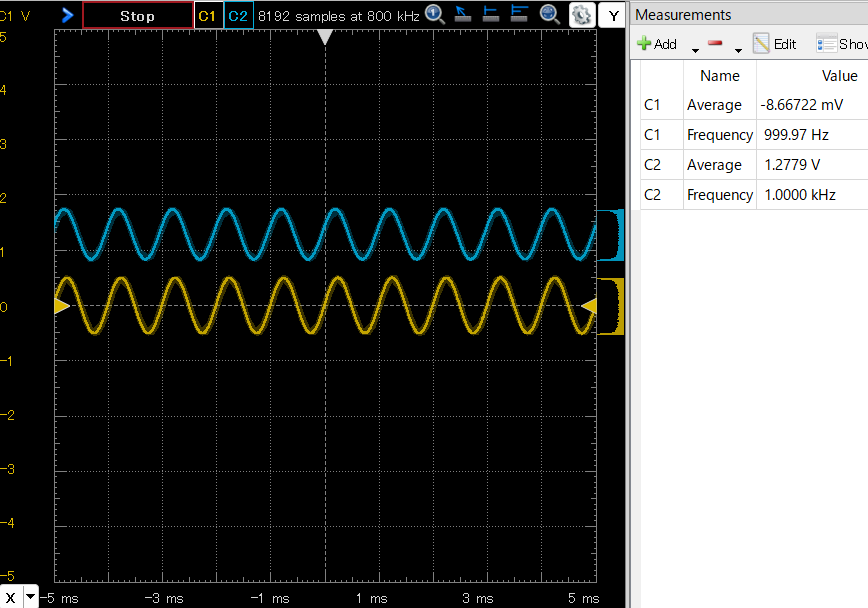
さて以下の回でやってみたとおり、上記波形はCSVファイルに輸出可能です。
お手軽ツールで今更学ぶアナログ(149) WaveForms、測定データのセーブあれこれ
なお、以下は御本家Digilent社のWaveFormsのマニュアルページです。
実際に上記から「輸出」したCSVファイルの一部を以下に示します。先頭部分に各種設定値などが#でコメント化されて出力されてます、データ自体はフツーのカンマ区切りです。
#Digilent WaveForms Oscilloscope Acquisition #Device Name: Discovery2 ~以下略~ #Negative Supply: OFF #Voltage: -1 V Time (s),Channel 1 (V),Channel 2 (V) -0.00511875,-0.3374237776010395,1.093392809139302 -0.0051175,-0.3337472829230979,1.097103841319657 -0.005116249999999999,-0.3337472829230962,1.100814873500012
CSVファイルの読み込みとプロット
以下のようにしてScilabで上記のCSVファイルを読み込んでみました。おまじない’!#!’は、#の含まれる行をコメントとして取り込めというお願いっす。読み込んだ後で、データの最初の4行をダンプするとともに、とりこんだコメント部分を表示してみてます。
filenameOSC0 = fullfile("C:\proj\analog\AD2toScilab", "OSC.csv");
[datOSC0, comments] = csvRead(filenameOSC0, [],[],[],[],'!#!';
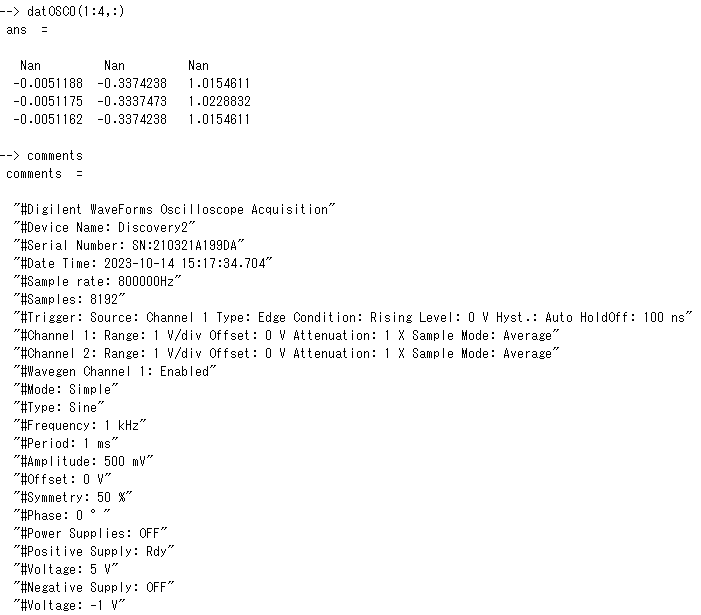
datOSC0(1:4,:)
comments
取り込んだデータは第1列が時間、第2列がチャネル1の電圧、第3列がチャネル2の電圧となっています。処理を分かり易くするために各列を個別の変数に代入してみました。こんな感じ。
t =datOSC0(:,1); ch1=datOSC0(:,2); ch2=datOSC0(:,3);
上記の後で気づいたのですが、データのトップにNaN(Not a Number)が鎮座してました。ヘッダ付きのCSVなのにその対処をしなかったためです。今回は、以下のようにして最初のNaNを読み飛ばして辻褄を合わせました。
t =t(2:8193); ch1=ch1(2:8193); ch2=ch2(2:8193);
次回以降は、CSVを読み取るときにヘッダ付きを指定すればNaNの発生は防げるであろうと(試してないケド。)
さて、データが読み込めたのでプロットしてみます。オペレーションは以下のとおり。
clf();
subplot(2,1,1);
plot(t, ch1);
xtitle("CH1", "time[s]", "voltage[V]");
subplot(2,1,2);
plot(t, ch2);
xtitle("CH2", "time[s]", "voltage[V]");
上記によるプロットが以下に。大分AD2画面とは違うけれどもプロットはできたみたい。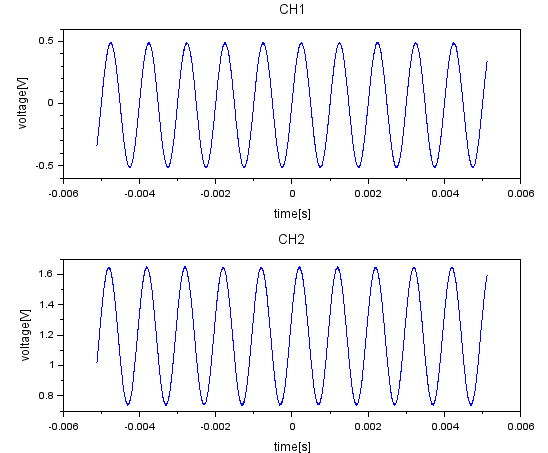
自己相関から周波数を求める
さて、プロットが出来ただけでは進歩がないので、Scilab関数を使ってちょっと処理をしてみます。使用してみるのは以下の関数です。
xcorr()
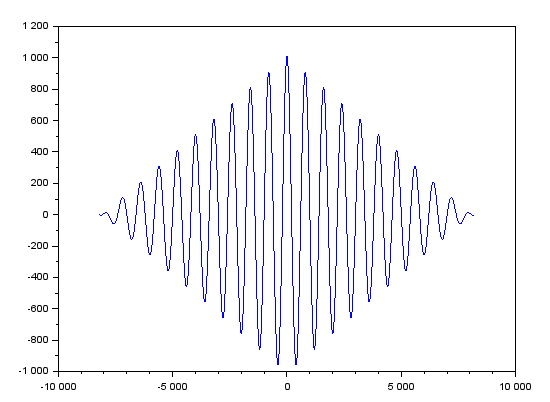
自己相関、相互相関を計算できる関数であります。まずはこれにch1(入力信号)を渡してプロットまでしてみます。
[c, ind] = xcorr(ch1); plot(ind, c);
自分自身と相関をとっているので、x軸のインデックスは0のときに最大値を与えます。これは当然。つづくピークは1周期「ズレた」ときの筈です。0のときと次のピークを拡大してみます。こんな感じ。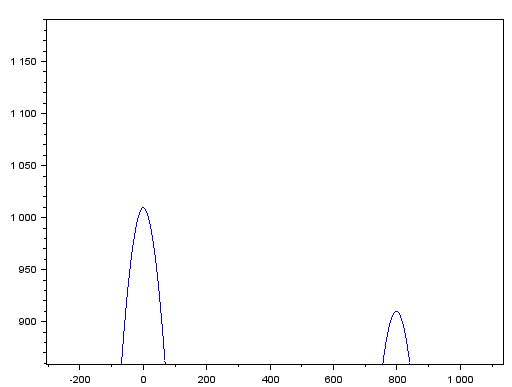
上記からするとインデックスゼロのときの次はインデックス800のときにピークがくるみたい。インデックス1の差に相当する時間は以下のTの計算から0.00125msecとな(以下では最初0.0000013などと丸めた値が表示されちまったので1000倍して正しい値を表示させてます。)
Tが分かったので、以下の計算をすれば、周波数Freqが求まる筈。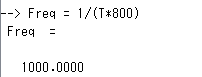
1000Hzデス。期待どおりね。
相互相関から位相進みを求める
つづいて、ch1とch2の相互相関を計算して、ch2の位相の進みを求めてみます。こんな計算でまずプロット。
[cx, indx] = xcorr(ch1, ch2); plot(indx, cx);
こんどは位相がズレた信号との相関とっているので、ちょっと「ひねくれた」グラフが出てまいりました。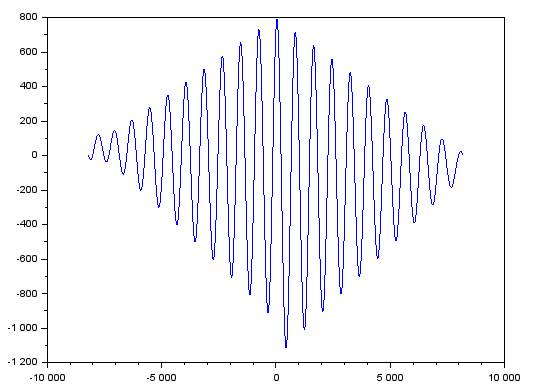
そのピークを拡大したものが以下に。測定ポイントを四角でプロットしてあります。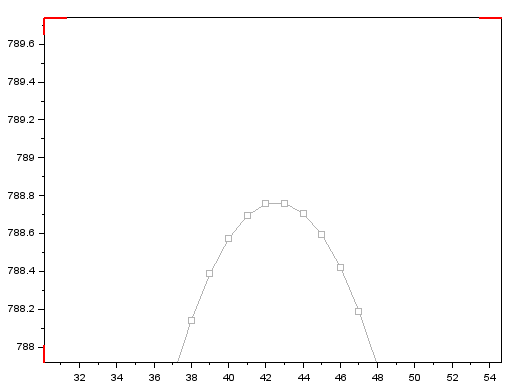
上記をみると、インデックスで42と43の間くらいにピーク(つまりそれだけ「ズラ」すとch1の波形とch2の波形が一番ピッタリくるということ)があるみたいです。インデックスでいうと1周期800であったので、以下を計算すると位相差(度)が求まる筈。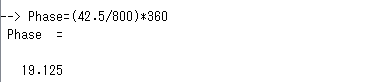
約19度の進みとな。まあそんな感じだな。いい加減。