前回は微分方程式の解曲線が「平面を覆う」こともあるの回でした。今回は先に解曲線群あって、そこから微分方程式を求めよの回デス。メンドクセー気がするのだけれども、まあ計算するのは例によってMaxima様なので、おまかせっと。お楽が一番。いいのかそういうことで。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
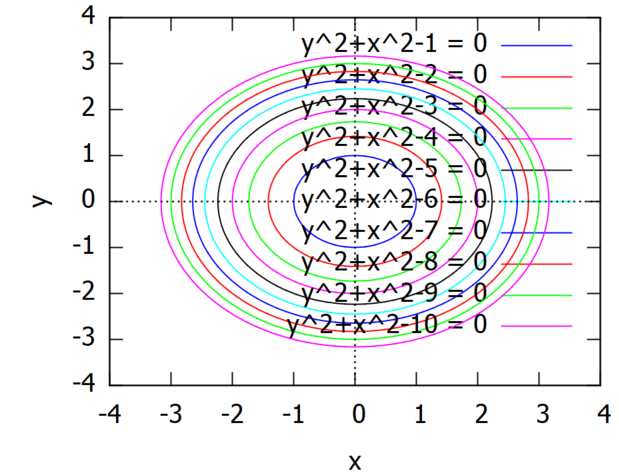
今回の例題はみんな知ってる原点中心の円の方程式です。ただrの2乗を任意定数Cとおいて、これをいろいろ変えたら平面を埋め尽くすだろ~と。多分ね。
そして解として円を得るような微分方程式をもとめよってこってす。
今回は先にプロットです。例によって10本ばかりの線を引いてお茶を濁してます。
plot2d(makelist(x^2+y^2-C=0,C, 1, 10), [x, 0, 5]);
「微分方程式」を求める
まあ先に曲線の式が与えられているので、これを微分すれば微分方程式になるみたいですな。ここで重要なのは、ただyなどと書くとyは只の定数なんじゃないかとMaxima様に解釈されそうなので、ことさらにY(x)のようにxの従属変数なんだ、と主張してみます。すると微分結果は以下のように。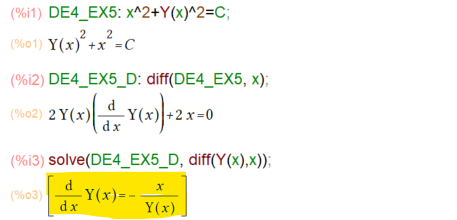
上記の黄色が求める微分方程式ですが、y’ = – x/y とシンプルに書いた方が教科書通りで座りが良いです。Maxima様にお願するにはシンプル過ぎるってことだけれども。