前回、1階/2階の常微分方程式の一般解を求めるときは無理やりdesolve関数に任意定数モドキを導入するよりODE2関数にお願いした方がスマートだということに気づきました。でも一般解をODE2関数で求めたとして、実際の値を代入して初期値問題とか解くときはどうするの?ちゃんと関数があったです。まずは1階、ic1とな。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
ic1関数
ぶっちゃけODE2の求める一階微分方程式の一般解にたいして、初期値問題を解くための関数がこれです。いつもお世話になっておりますMaxima様の日本語マニュアルの該当箇所が以下に。
今回の例題
今回の例題は 微分方程式 y’=y(1-y) において以下の3種の初期条件を満たす解を求めよというものです。
-
- y(0)=1/2
- y(0)=2
- y(0)=1
ただし、上記の3番についてはそのままic1使って解こうとすると以下のようなエラーに遭遇することになります。
最初の微分方程式みたら分かるけどね、右辺のy(1-y)にy=1代入したらy’=0です。傾き0の直線。
ODE2で一般解を求める
今回は、ODE2一撃ではy=…の形にはできず、ふた手間かけてます。こんな感じ。
教科書的にはべき乗のところに+%cでなく、係数に%cの方が良いみたいですが、以下の処理みるとMaxima様的にはこのままでOKじゃないかと思います。
さてic1関数を使って上記の1と2のケースの初期値問題を解くと以下のごとし。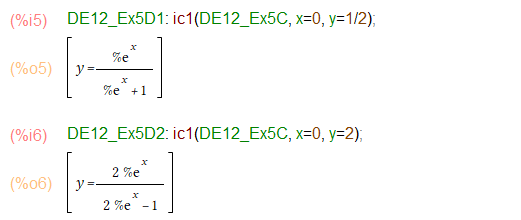
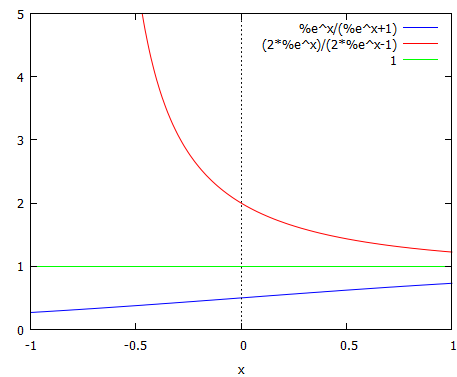
上記の1、2番目の解と先ほどの3番目のペッタンコな(y=1)解をグラフにする操作は以下に。
ほんとテキトーだけれどもカッコはついた?新年そうそういい加減。