前回に続きBootパッケージ中のgravityサンプルデータセットです。このデータセットは「人気者」にて、Bootパッケージの中の数ある処理関数の約４分の１が処理例に使ってます。しかしなあ、ブートストラップ法どころか統計素人の老人がBootパッケージの奥底に潜っていくのは辛いっす。なんだか分からんよな。
※「データのお砂場」投稿順Indexはこちら
重力加速度の測定方法
前回はgvavityデータセットの重力加速度の測定には振り子使っているみたい、ということでさらっと通り過ぎてしまいました。だいたい米国の国立標準局（現在のNIST）が測定したデータということでキッと立派な方法なんだろ～的鵜呑みでした。結局は、高校（中学？）で習う振り子の周期Tの以下の式に帰着するのだろう、と。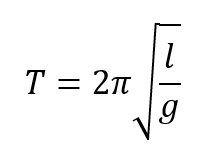
しかし考えてみると、振り子の長さｌってどうやって測ればいいの。糸の先に重りをつけたとしても重りにも大きさはあるので重心位置？支点は支点で釘に糸を縛っても実際にはどこだ？結構メンドイ感じがありありです。
しかし調べてみたら、この重力加速度の測定につかう「可逆振り子」、発明者のお名前付きの歴史と伝統あるものでした。米国『HARVARD UNIVERSITY』様の以下のページに詳細が説明されています（物理学実験の説明ページ？）
上記を読んでようやく腑に落ちた感じっす。ホントか？
abc.ci
さて今回処理例をなぞってみるのは、abc.ci（Nonparametric ABC Confidence Intervals）という関数です。abcってなんじゃらほい、と思って読んでみると
abc = approximate bootstrap confidence みたい
です。bootstrap confidence Intervalsを計算するのだけれども、approximateなのね。。。解説ページが以下に。
Nonparametric ABC Confidence Intervals
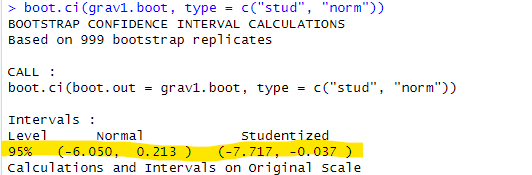
前回、boot.ciという関数で信頼区間の計算を２種類もやった気がするのですが、ここでこれとは異なる算法が現れいでたと。素人にはその差が良く分かりませぬ。しかし、
-
- boot.ciでは、まずboot関数で処理した結果を与える必要があった
- abc.ciでは、boot関数など飛ばして最初から計算できる
ということでまず手順からしてお手軽。approximateのお陰？また、関数の中で呼び出す統計量を計算する関数の定義もお楽みたい。個人的にはこちらの方が好きだな～。まあ計算法が違うので同じ意味ではないけれども。
早速処理例を実施。こんな感じ。
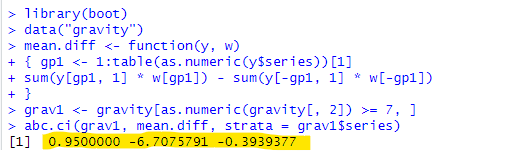
お答えの３つ組の数字は左から95%信頼区間で、実験の７番目と８番目の系列の差の平均の下限、上限ってことみたいです（前回やったとおりで、gravityには８つの微妙に異なる設定での実験結果が詰まっており、その最後の７番目と８番目を比べるお約束です。）
念のため、前回boot.ciで求めた信頼区間が以下に。
素人には似たような数字に見えるが。。
なお、abc.ciのデフォルトは95%ですが、簡単に変更もできるみたい。こんな感じ。
90％でよければもっと信頼区間は狭くなるわいな。
後７個も処理例を掘る元気ないっす。