前回は第2のFIRフィルタ設計関数wfirでFIRフィルタを作製してみました。GUI(wfir_gui)はイマイチ(個人の感想です)だけれども「フツーに便利」な感じっす。今回は第3のFIRフィルタ設計関数ffilt関数を使ってみます。こいつが一番シンプル?な関数なんだけれども秘密?、謎?も多い(個人の感想です。)
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上で、Scilab6.1.1およびScilab上のツールボックス Scilab Communication Toolbox 0.3.1(以下comm_tbx)を使用させていただいとります。
ffilt関数
以下にffilt関数のマニュアルページへのリンクを貼り付けておきます。
上記マニュアルページには「FIRローパスフィルタの係数」と説明が書かれているのですが、すぐ下の引数の説明みると、ローパスだけでなく、ハイパス、バンドパス、ストップバンド全て含まれとります。どゆこと? 歴史的な経緯でそのような記述が残っているのか、それともどちらかが間違っているのか。。。
この関数がちょいと謎なのは、フィルタ係数を求める算法です。過去
-
- fsfirlin関数、周波数標本法
- wfir関数、ウインドウィング法
などと記載がありました。信号処理素人の年寄にはサッパリですが、算法への手がかりはあると。まあ結局のところこの老人のような凡人は自分で手を動かすか、せめてプログラム書いて計算してみない限り身に染みて分かることはないんでありますが。例によって生成AIなどに「周波数標本法について教えて」などとお願いすれば、それらしいことを教えてくれるっと。ホントか?
しかし、ffilt関数については上記のような算法への言及まったくありませぬ。ソース読んだら分かるでしょ論法か? その気力はまったくなし。。。
「とりあえず」今回はローパスフィルタをこさえてみます。前回 wfir関数のときもローパスだったので、似たような設定でフィルタを作って比較してみるつもりです。
今回実験のScilabコード
ffilt関数を使ってローパスフィルタ1個を定義し、その周波数応答をグラフにしてお茶を濁そうとするものです。なお、生成するフィルタは前回と「なるべく同じ」条件です。
-
- ローパスフィルタ
- フィルタの次数33(N=33)
- カットオフ周波数(正規化周波数で)0.2
前回のwfir関数では、どんな窓関数を使って無限につづくインパルス応答を有限の範囲に切り取るのか窓関数の指定があったのですが、今回は無です。おまかせ。
x=ffilt("lp",33,0.2);
[xm, fr]=frmag(x, 1, 255);
clf;
plot(fr, 20*log10(xm));
xlabel("Normarized Frequency");
ylabel("Gain[dB]");
title("FFilt(LPF N=33 Cutoff=0.2)");
生成したフィルタの特性
上記のコードで生成したフィルタ(変数ベクトルxに格納される)の特性が以下に。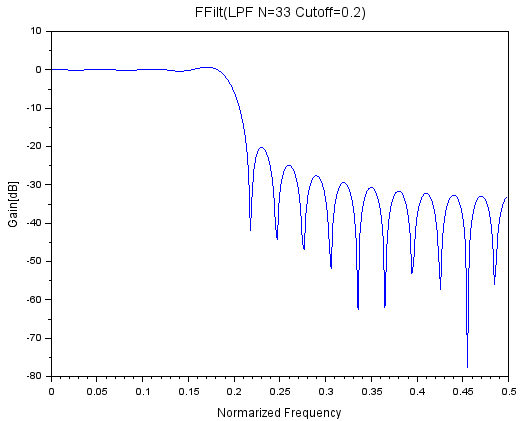
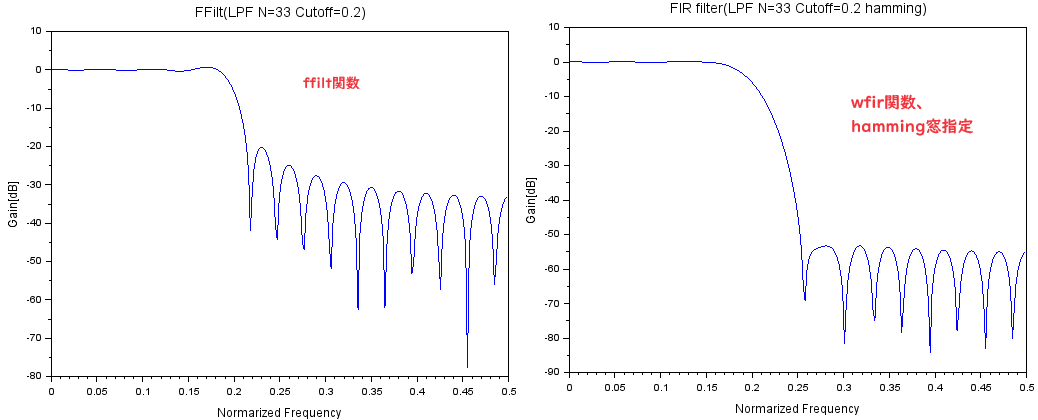
確かにカットオフ周波数0.2Hz(正規化)のフィルタが出来ているみたい。明らかに前回wfirでハミング窓を使って作ったフィルタとは特性が違う。。。あたりまえか。