今回から連続時間パレットの練習に入ります。こここそはXcos使う上での真髄的なもののひとつらしいっす。連続時間＝微分方程式系で書き表せるもの、あるいはラプラス演算子sで書き表せる連続系の伝達関数を用いて表現できるものです。デジタル計算機の上で計算しているのだけれども、表向きはソルバ様が頑張って連続に見せてくれるのね？
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11のパソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
「連続時間システム」パレット
パレットの全貌が以下に。他のパレットに比べると大した数のパレットが並んでいるわけではないけれど、歯ごたえのありそうなものどもが並んでます。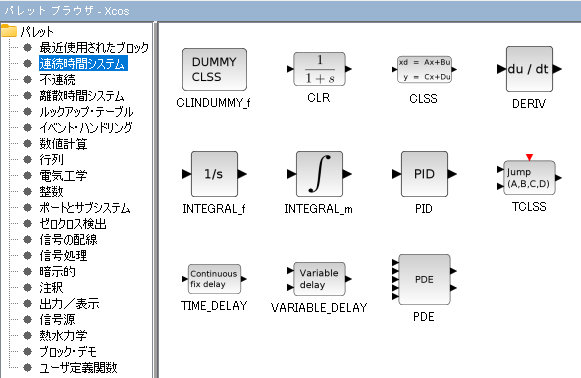
上記のやつらを練習していきたいと思いますが、今回は上記の中でも「お手頃な」以下の５つの基本的なブロックどもをやっつけたいと思います。ヘタレだなあ～。
-
- INTEGRAL_m、入力の時間関数u(t)を積分
- INTEGRAL_f、入力の時間関数u(t)を積分
- DERIV、入力の時間関数u(t)を微分
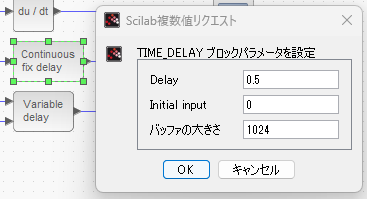
- TIME_DELAY、入力の時間関数u(t)を定数時間遅延
- VARIABLE_DELAY、 入力の時間関数u(t)を可変時間遅延
積分が二種類もありますが、以下のところが違います。アイコンが違うのですが機能も違うっと。
-
- INTEGRAL_mは、積分記号のアイコン。ある値の範囲にサチュレーションさせたり、再初期化を行ったりすることも可能。イメージ的にはオペアンプで作った積分器のような物理的な動作をさせられる。
- INTEGRAL_mは、ラプラス演算子sを使った “1/s” のアイコン。初期値以外は指定できない。あくまで算術的な？
なお、ご本家の簡潔明瞭な（素っ気ないともいう）HELPページは以下です。
Continuous time systems palette
今回実験のフロー
今回実験のフローは入力関数 u(t)=1.5*sin(2πt) とした正弦波を上記の５つのブロック全てに入力し、その出力を観察するというものです。全体フローが以下に。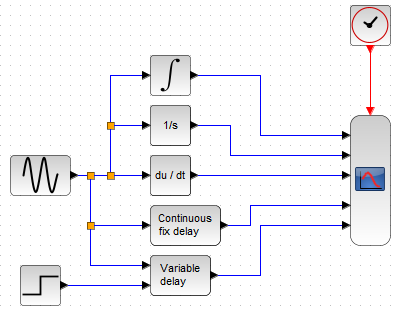
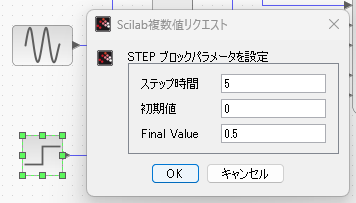
なお、VARIABLE_DELAYは可変時間の遅延をさせるのに何か関数が必要なので、シミュレーションの途中で突然変わるステップ関数を使って遅延時間を変化させてます。
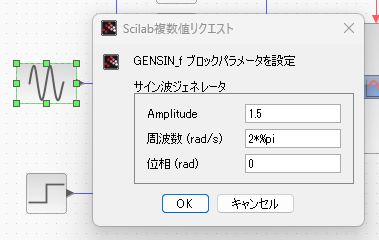
大本の正弦波ブロックの設定が以下に。
上記での振幅はオフセット中心の所謂振幅で、ピークツーピークの値ではありません。ScilabのHELP読んでいるとまれにピークツーピークの値を振幅と書いているページがあるので気を抜けませぬ。コマケー話だけれども。また、周波数が(rad/s)なのも数学できるヒト系だよな。現場的にはHzが好きなんだけれども。
可変遅延を与えるためのステップ関数の設定が以下に。
各ブロックの設定
まずは「積分記号」アイコンのINTEGRAL_mブロックの設定。０から0.25の範囲にサチュレーションさせてます。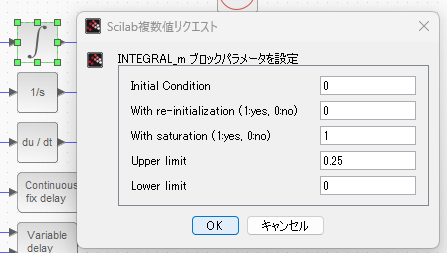
つづいて「1/s」アイコンのINTEGRAL_fブロックの設定。デフォルト設定のまま。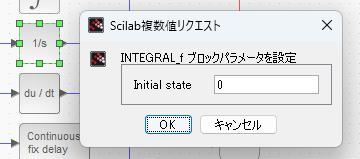
続いて微分のDERIVブロックですが、このブロックには設定ウインドウがありません。今回は、1.5*sin(2πt) という波形を微分するので、当然cos(2πt)が現れますが、忘却力の年寄はその振幅を計算できません。ということで別シリーズ「忘却の微分方程式」でいつもお世話になっているMaximaに計算してもらいましたぞ。だいたい9.4くらいになるのね。。。
つづいて定数時間の遅延、TIME_DELAYの設定。
最後は可変時間の遅延、VARIABLE_DELAYの設定。
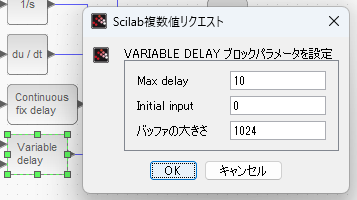
入力遅延の最大は0.5だからMax delay10なんていらないのだけれども。。。
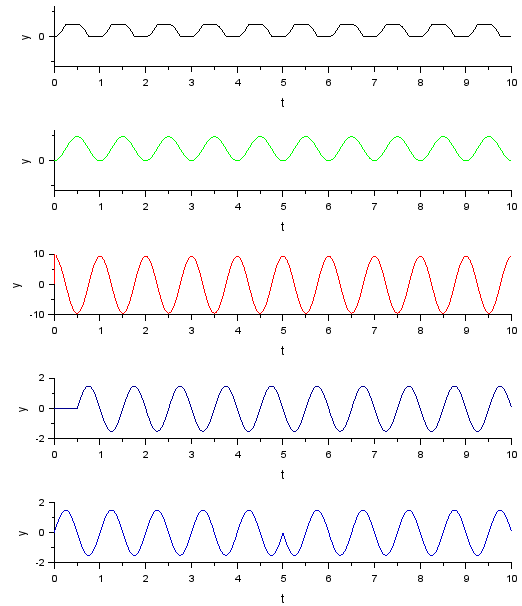
シミュレーション結果
上のグラフから、順番です。
一応、予定通りの波形が出ているみたい。次は、手強そうな奴らが残ってるな。。。大丈夫か。