頼り切ってきたode2関数が前回より使えなくなり、どうなることかと思いましたが、何とか乗り切った？感じです。今回は前回の続きの例題を解いて（実際に解くのはMaxima様ですが）みます。まあ、一度「型」がきまってしまえば以下同文と。何時のまにか３階どころか４階の方程式も解けるようになっていたっと。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
例題２
前回につづき、desolve()関数（内部でラプラス変換しているらしいです）で一般解を求めたいとおもいます。微分方程式は三階です。とりあえずatvalue()関数で、初期値に定数を当てはめておきます。K0、K1、K2っと。
これをdesolveすれば上記のように微分方程式の解がもとまりますが、ちょっと煩雑なので、上の赤丸のように係数をまとめてC1、C2、C3などとしたいと思います。
上記黄色のマーカーが、教科書的に整理？したお答えです。C1、C2、C3を定義するときにわざわざcoeffつかってK0、K1、K2と橋渡ししたので、ev()関数に黄色のマーカの解を渡せば元の形に戻すことも可能。
例題３
続く例題は４階です。でもやり方は一緒。
求まった解の各係数をC1、C2、C3、C４なる定数でまとめたいと思います。今回はわざわざKxとの変換など考えず、単純に人手で書き変えるだけ。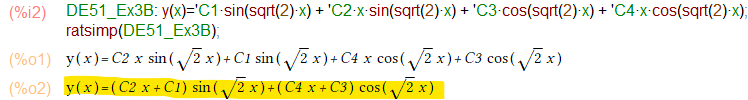
最後にちょいと ratsimp()関数で形を整えれば教科書的な形になりました。