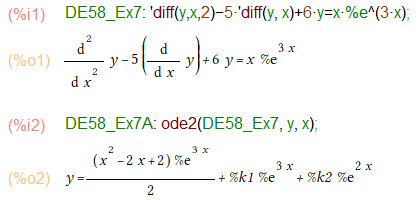前回は「非同次」の2階線形微分方程式の「右辺Q(x)」が特定の形のときに未定係数法で解けるという例題を練習。といって実際には教科書がお教えくださっている手順を「スルー」、2階ならば使える伝家の宝刀ode2にお任せでした。今回はさらに2階の「非同次」方程式の例題を解くのですが、今回も「ode2お任せ」ぞなもし。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
Q(x)が積の形でも未定係数法は有効だぞと
ターゲットの定数係数非同次線形微分方程式は教科書的には、こんな感じの「奴」です。
y” + ay’ + by = Q(x)
前回は、Q(x)が多項式、三角関数、指数関数の3種類ならば未定係数法つかって特殊解を求めることができ、そこから一般解が求まるという手順でした。けれども 伝家の宝刀 ode2() はその辺の「事情は全部お見通し」です。一撃で一般解が求まります。
今回は、前回のフォロー的なやつ。Q(x)が、多項式、三角関数、指数関数を組み合わせた積の形でも同じやり方で解けるぜ、というところ。教科書的にはかなりスペースを使ってその解き方をお教えくださっているのです。ありがたや。
例題7
以下の例題は、Q(x)=x * e3*x という「多項式」と「指数関数」の積の形です。しかし ode2()にそのままお願いすれば一般解が求まってしまいます。
ただし、上記の解の形はチョイと教科書とは違います。上記では e3x の定数係数 を整理しなおすと %k1 + 1 となるのですが、これを一つにまとめて定数としてます。そこで以下のように ratsubst() して、expand()してみました。これで%k1 + 1を1個のC1という定数にまとめられたっと。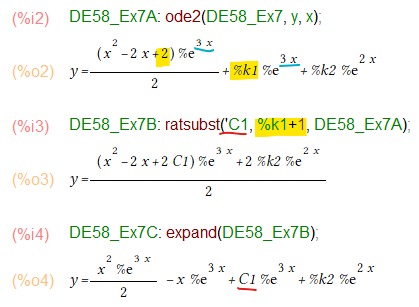
いままでsubst()は使ってましたが、こういうときにはratsubst()使うと良かったのね。後処理の変形方法、微妙に向上した?