前回は「超越関数」のうち三角関数の計算例でした。まだ逆三角関数が残っているのだけれど見ないフリをして先に進めます。今回は指数関数です。フツーの関数電卓などでは x^y 的なボタンがあって一撃なのだけれど、8087においてはそうは問屋が卸してくれません。指数関数の底の変換公式が登場。忘れているよゐこは思い出さないと。
※「ぐだぐだ低レベル プログラミング」投稿順indexはこちら
※実機動作確認(といってもエミュレータなんだけれども)には以下を使用させていただいております。
※オリジナルの8086+8087の組み合わせでは8086と8087の同期をとるためにWAIT命令が必用になる場合があります。後継機種ではWAIT命令が不要(演習に使用しているエミュレータQEMUでも不要)なのでWAIT命令は使用しません。メンドイし。
F2XM1命令
指数関数を計算するのに、8087が用意してくれている命令はF2XM1という以下のような計算をする命令が一つだけです。
2^x – 1
2の「スタックトップの値」乗ひく1を計算してくれるもの。勿論、Fを頭にいただく命令である以上、入力オペランドとなる指数 x は浮動小数でOKです。ただし、オペランドの範囲の制限はキツイです。これを超えるとNaNが返る筈。
-
- 8087、80287:オペランドは0≦ x ≦0.5
- 80387:オペランドは-0.5≦ x ≦0.5
- 以降のプロセッサ?:オペランドは-1.0≦ x ≦1.0
小数点以下のべき乗のところはメンドーみてやるから、小数点以上の部分はプログラマ様がよきに計らってね、という感じ。
そして、2のべき乗しか計算できないじゃん、ということではまったくありません。昔(高校?中学?)習った筈の、指数関数の底の変換公式を思い出せよ、ということらしいです。
\( y^x = a^{x log_a y} \)
そして8087は、以下の定数を内部に持っているのでアリガチな 10のべき乗や、e(自然対数の底、ネイピア数)のべき乗は変換公式で一撃であると。
-
- FLDL2T命令=定数 log_2(10)
- FLDL2E命令=定数 log_2(e)
なお、任意のYについてのlog_2を求める方法は次回の対数関数でやる予定です。それがあれば、yのx乗もバッチリ、ホントか?
今回実験のプログラム
さて今回実験のプログラムは、以下の「小さい」指数の指数関数値を各1点づつ計算するというものです。勿論上記の「指数関数の底の変換公式」を利用。
-
- 10^0.1 = 1.2589254117941672104239541063958
- e^0.1 = 1.1051709180756476248117078264902
なお、やたら長大な値が書かれているのは、Windows付属の関数電卓で計算した結果です。上記の数字に「似た」数字が返ってくれば、実験プログラムはまあ良しとするかと。
なお例によって強力なx86用アセンブラNASM用のソースです(MSのMASMともインテルASM86とも微妙に異なるけど、まあ分かるっしょ。)
%use fp
segment code
..start:
mov ax, data
mov ds, ax
mov ax, stack
mov ss, ax
mov sp, stacktop
test:
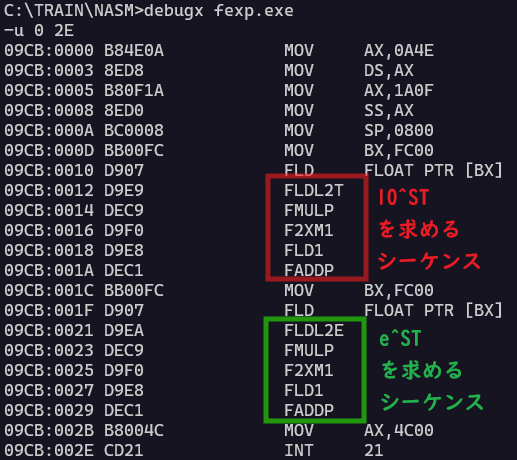
; 10^[src1 = 0.1]
mov bx, src1
fld dword [bx]
fldl2t
fmulp
f2xm1
fld1
faddp
; e^[src1 = 0.1]
mov bx, src1
fld dword [bx]
fldl2e
fmulp
f2xm1
fld1
faddp
fin:
mov ax, 0x4c00
int 0x21
resb 2048
segment data align=16
resb 1024 * 63
src1: dd 0.1
segment stack class=STACK align=16
resb 2048
stacktop:
dw 1024 dup (0)
stackend:
アセンブルして実行
MS-DOS互換で機能強化されているフリーなFreeDOS上、以下のステップで上記のアセンブラソース fexp.asm から実行可能なオブジェクトファイルを生成して実行することができます(nasmとwatcom Cがインストール済であること。)
なお、FreeDOS付属の「debugx」デバッガは、8087のレジスタ内容を浮動小数で見せてくれます。
nasm -f obj -l fexp.lst fexp.asm wlink name fexp.exe format dos file fexp.obj debugx fexp.exe
10の0.1乗(0.1はスタックトップに格納)を求めた後の様子が以下に。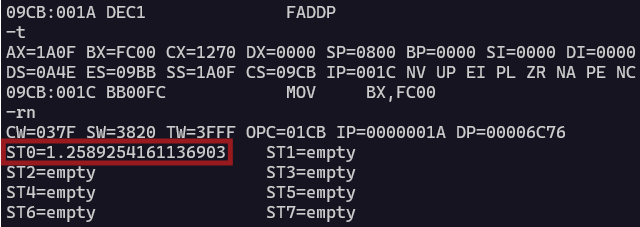
eの0.1乗(0.1はスタックトップに格納)を求めた後の様子が以下に。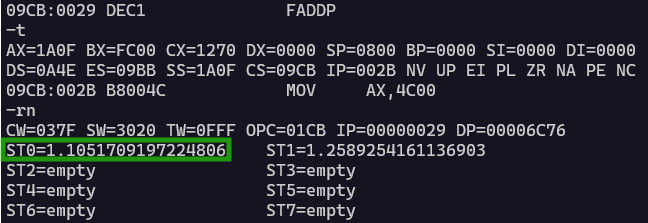
まあ、10のべき乗も、eのべき乗も求まることは分かった。次回は対数関数じゃね。