前回はScilab上で「離散時間信号」ぽいプロットができるようになったので、今回は「離散時間信号」ぽい入力信号を生成する関数を準備したいと思います。必要に迫られてその場その場で「誤魔化して」きたのが今までの実体。これを反省、事前にある程度「汎用」に使える「信号源」を用意しておこうという目論見です。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※実習に使わせていただいている Scilab処理系は 6.1.1 (Windows版)です。
今回は関数定義なので、以下のScilabのオンライン日本語ヘルプページを参照させていただいております。
functions Scilab プロシージャおよび Scilab オブジェクト
とりあえず準備する「波形」
思いつくまま(こういうところが泥縄ですが)、以下の5つの波形を事前準備することにいたしました。まあ、足らないところがあれば順次追加するという方針であります。
-
- 正弦波
- 矩形波
- 三角波
- インパルス信号
- ステップ信号
正弦波には位相もパラメータにいれましたので、Sine、Cosineどちらでもいけることはいうまでもありませぬ。
基本以下のようなパラメータを与えて波形を生成するものとしました。
-
- サンプリング周波数[Hz]
- サンプル点数
- 周期信号はその周波数[Hz]
- 振幅(マグニチュード)
- 波形により位相など他のパラメータもあり
関数の返り値は、2つの1次元配列(ベクトル)です。第1の配列が時刻[単位秒」を保持するもの。第2はその時刻での値を保持するもの。
正弦波(サイン波)
作成した関数が以下に、周波数と位相、振幅を指定できるので必要十分かと。同じ時系列で複数周波数を生成すれば足し合わせることも可能なハズ。
// Generate Sine wave
// Fs: sampling frequency [Hz]
// nSample: number of samples
// fq: frequency [Hz]
// phdeg: phase [deg]
// mag: manitude
function [t,y]=genSin(Fs, nSample, fq, phdeg, mag)
t = ((1:nSample) - 1) / Fs;
y = mag*sin(2*%pi*(fq*t+(phdeg/360)))
endfunction
上記の関数をScilabに読み込み後、以下のように呼び出せば、サンプリング周波数1000Hzで周波数10Hz、位相0度、振幅1の正弦波を100点分得ることができます。
[t,y]=genSin(1000, 100, 10, 0, 1); plot2d3(t, y);
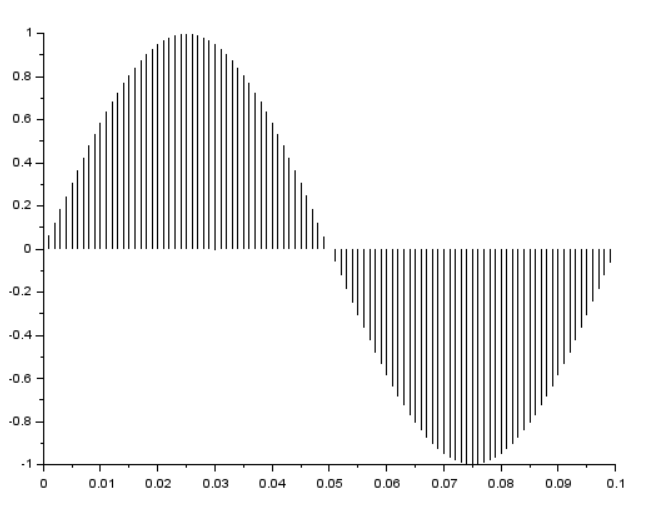
コサイン波を得るために位相を90度ずらし、また周波数を倍、振幅も倍にしてみたものが以下に(サンプリング周波数は10000Hz)
[t,y]=genSin(10000, 200, 100, 90, 2); plot2d3(t,y)
プロットが以下に。
方形波(矩形波)
上記の正弦波のパラメータを踏襲の上、デューティ比[%]を与えて方形波を生成する関数が以下に。
// Generate Square wave
// Fs: sampling frequency [Hz]
// nSample: number of samples
// fq: frequency [Hz]
// phdeg: phase [deg]
// mag: manitude
// duty: [percent]
function [t,y]=genSquare(Fs, nSample, fq, phdeg, mag, duty)
t = ((1:nSample) - 1) / Fs;
tx = 2*%pi*(fq*t+(phdeg/360))
y = mag * squarewave(tx, duty)
endfunction
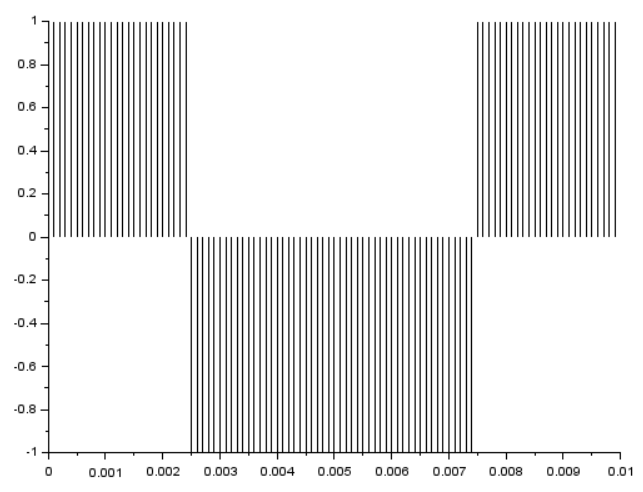
上の関数を使い、サンプリング周波数10kHzで、100Hz、振幅1、位相90度、デューティ50%の矩形波を生成する場合。
[t, y]=genSquare(10000, 100, 100, 90, 1, 50); plot2d3(t,y);
プロットが以下に。
三角波
三角波は上記の矩形波関数を元に作ったのですが、ついにFor文使ってしまいました。For使わないでもできるみたいですが、頭がついていかないので、べたに「積分」的な足し算で三角波を作ってます。ダメだな。。。
※2023年12月21日追記:以下の関数で0度以外の位相を与えるとオフセットが載ってしまうことが今更ながら発覚。第111回にて修正した関数を作ってます。
// Triangular wave
// Fs: sampling frequency [Hz]
// nSample: number of samples
// fq: frequency [Hz]
// phdeg: phase [deg]
// mag: manitude
// duty: [percent]
function [t,y]=genTriangular(Fs, nSample, fq, phdeg, mag)
dmag = mag * fq / Fs;
t = ((1:nSample) - 1) / Fs;
tx = 2*%pi*(fq*t+(phdeg/360));
yd = dmag * squarewave(tx, duty);
sum = 0;
for i=1:nSample
y(i)=sum+yd(i)
end
endfunction
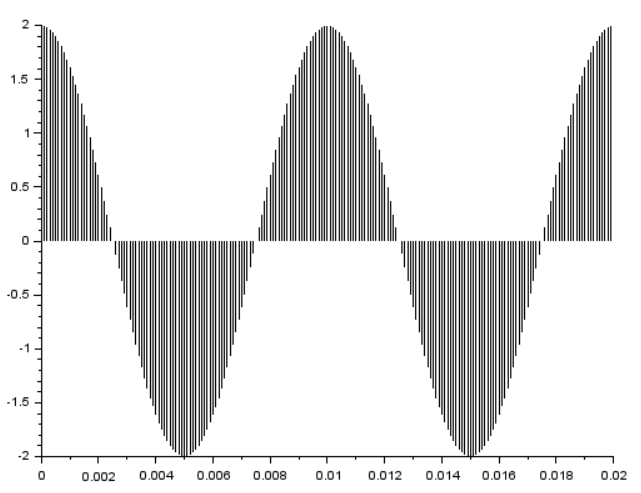
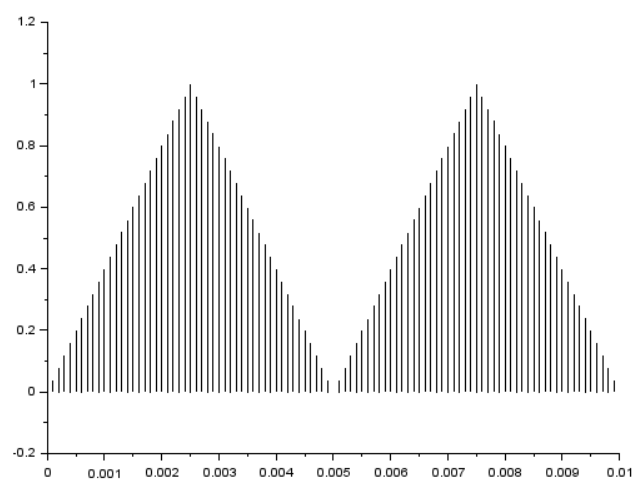
以下のプロットの三角波の設定が以下に。これだけ振幅が0になってます。
[t, y]=genTriangular(10000, 100, 100, 0, 1);
あとでもっとカッコいい方法を考えよう。
インパルス信号
インパルス信号は、何サンプル目に一発載せるか指定。振幅を1にすれば単位インパルス信号。
// Generate Impulse signal
// Fs: sampling frequency [Hz]
// nSample: number of samples
// nPos: Impluse position
// mag: manitude
function [t,y]=genImpulse(Fs, nSample, nPos, mag)
t = ((1:nSample) - 1) / Fs;
y = zeros(1,nSample);
y(1, nPos) = mag;
endfunction
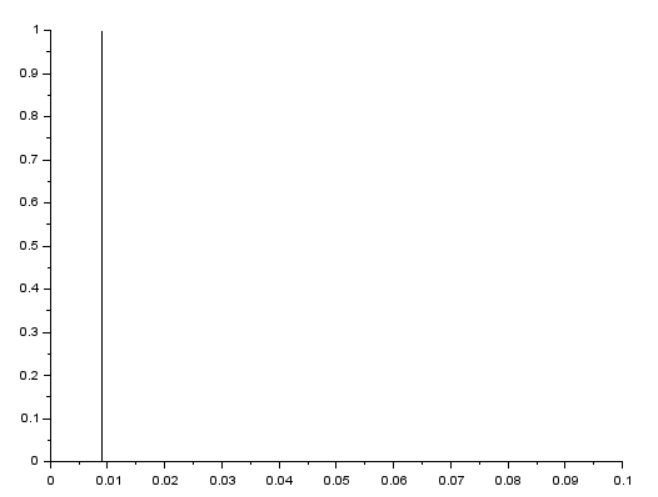
単位インパルス信号の生成の指定。サンプリング周波数1kHzで10サンプル目に一発載せるっと。
[t, y]=genImpulse(1000, 100, 10, 1);
ステップ信号
上記のインパルスをそのあと継続すればステップに。
// Generate Step signal
// Fs: sampling frequency [Hz]
// nSample: number of samples
// nPos: Step position
// mag: manitude
function [t,y]=genStep(Fs, nSample, nPos, mag)
t = ((1:nSample) - 1) / Fs;
y = zeros(1,nSample);
y(1, nPos:nSample) = mag;
endfunction
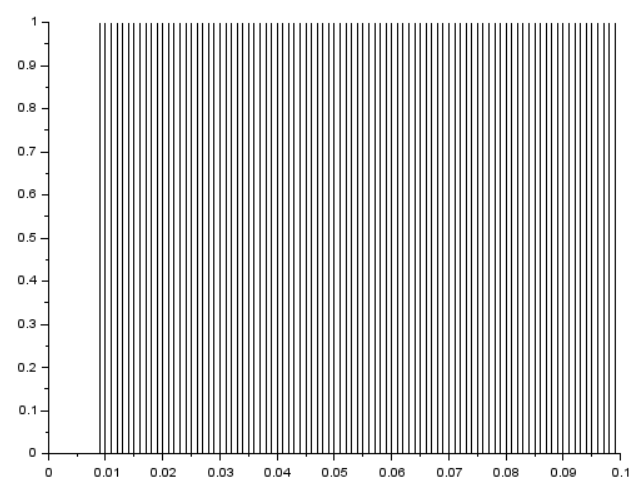
サンプリング周波数1kHzで10サンプル目でステップと。
[t, y]=genStep(1000, 100, 10, 1);
たった5つ作るだけで、途中ずいぶん間違えました。まだ間違いあるかも。泥縄で直すのだなあ。