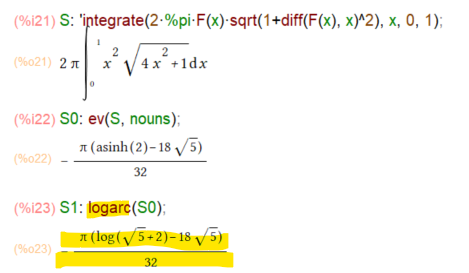前回につづき、Maxima様にお願いするなら「計算を簡単にするためのコマケーテク」など不要、そのまま計算すればOKよ、の回なんであります。折角教科書はテクを教えてくれているのに。しかし積分結果に逆双曲線関数登場。あれあれ、逆ハイパボリックサインってどんな関数だったっけ？log()の形に変形したいのよ。どしたら良いの？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
回転体の側面積を求める公式
今回は普通の定積分です。このところ、二重積分、三重積分ばかりだったのでスッキリしてるな～。今回使用してみるのは以下の公式であります。
なぜこうなるのか知りたい人は上記の教科書をご覧くだされや。
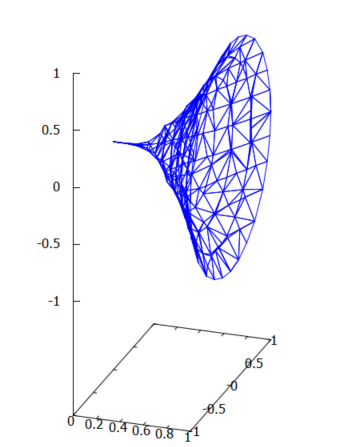
今回の例題とそのプロット
さて今回の例題は、以下のF(x)をx軸周りに回転してできる回転体の側面積Sを求めよというものです。
３次元空間の中でyz平面を考えると、真ん中のｘ軸を中心の円になるに決まっているので、グラフを描くのであれば
y^2+z^2=F(x)^2
だということが分かります。
F(x):=x^2; draw3d(proportional_axes=xyz, implicit(y^2+z^2=F(x)^2, x, 0, 1, y, -1, 1, z, -1, 1));
グラフが以下に。末広がりでラッパ風？
グラフに描けるのであれば、きっと計算できる筈。ホントか？
積分すれば答え一発？
教科書では「ちょいテク」使って計算を簡単にしているのですが、前回の教訓に基づき、今回は素のまま処理してみます。こんな感じ。
S: 'integrate(2*%pi*F(x)*sqrt(1+diff(F(x), x)^2), x, 0, 1); S0: ev(S, nouns);
ただし、下の方の計算を見ると上記のお答えには asinh()、逆ハイパボリック・サインなる不穏な者が登場。きっともっと分かったような気になれる関数を使って書けるのだと思うケド。。。
そこで結果を以下のように処理するとasinh()が消えてlog()になります。
S1: logarc(S0);
実際、Maxima様に計算をお願いしたところが以下に。
なお、逆双曲線関数表示を「同値の」対数関数に置き換える logarc()関数については、Maxima様の以下のマニュアルページ（日本語）に説明されとります。
一撃で計算するのは良いのだけれど、期待の表現とは「一味違う」表現で返してくれることがあるのよね。