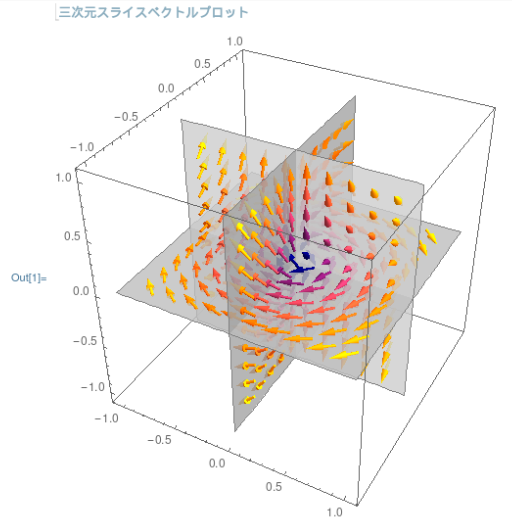
前回、勾配とか発散とかベクトル解析らしきことを少しやってみましたが、今回は、ベクトル場の図示です。Mathematica、カッコよく描けるのだけれども、非力なラズパイ３の限界を感じてしまいました。Maximaは３Dでやるのは面倒そう（やらないケド。）
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版）です。Mathematicaはラズパイ上の12.2.0.0です。
学生でもないのに勝手に参照させていただいておりますのが、Wolfram社Mathematicaの以下のチュートリアルです。
数学を学ぶ学生のための入門チュートリアル ベクトル解析と可視化
対するに Maximaの方は、以下のマニュアルページを参照させていただきました。
２次元でのベクトルプロット
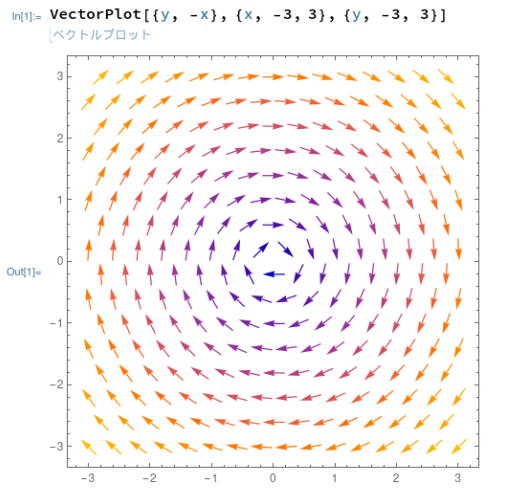
例によってMathematicaの場合、そのものズバリのお名前の関数が良いされているので、それを使えばベクトル場のプロットは簡単です。そして、特にオプション指定などしなくても、「カッコよく」描いてくれます。こんな感じ。
一方、Maximaのplotには矢印を描く機能がありますが、「ベクトル場」をもらって矢印を作り出しながらプロットするような機能は素のままでは無いみたいです。そこで外部のライブラリファイルを読み込んで使うことになります。
上記のMathematicaと同様な図を描くための命令が以下に。
load(plotdf); plotdf([y, -x],[x,-3,3],[y,-3,3]);
これにより別ウインドウ plotdfが開いて、以下のようなプロットが現れました。何もオプション指定しないとちと素っ気ない感じがしますな。
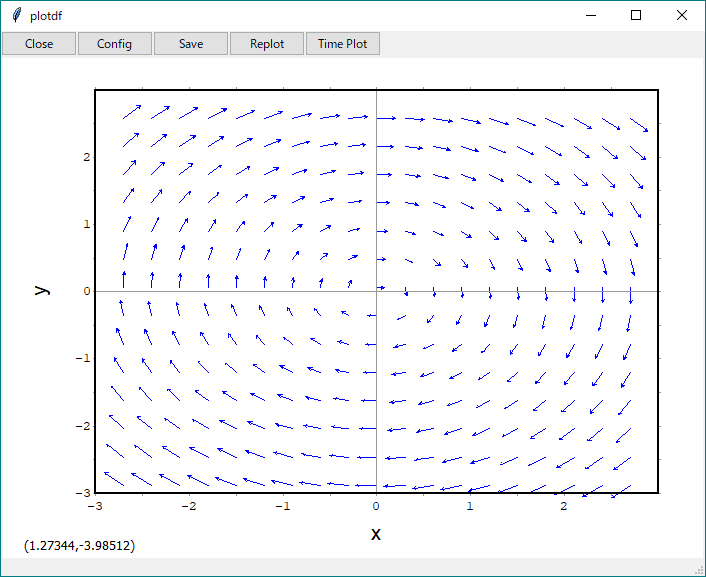
Mathematicaと違って別ウインドウですが、ベクトルプロットは得られた、と。
３次元でのベクトルプロット
ベクトルの始点、終点からなるリストを前もって計算しておき、それをプロットするようにすれば Maximaでもプロットできないこともない（実際にはgnuplotにお願いしているのだけれど）ような気がいたします。しかし確かめる元気もありません。Maximaでの３Dベクタプロットはパス。
さて、Mathematicaにはまたしてもそのものズバリの３Dベクタプロット関数がありました。こんな感じ。
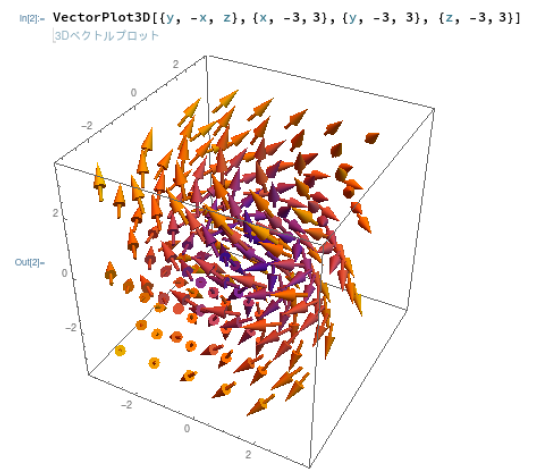何もオプション指定しないのに、このカッコよさはなかなかのモンです。しかし、Raspberry Pi 3 Model B＋（Raspbian OS 32bit)上の「無料」Mathematicaでは、時間かかります。「秒」とはいかなくて「分」という感じ（正確に測ってないです。）せめて Raspberry Pi 4 でやりたいと思いました。
しかし上記はカッコいいですが、ちょっとゴチャゴチャしすぎて、いったいどんな風に「流れているのか」良く分からないデス。そんなときに使うのであろう、Slice化した3Dプロットというのもありました。それがこちら。
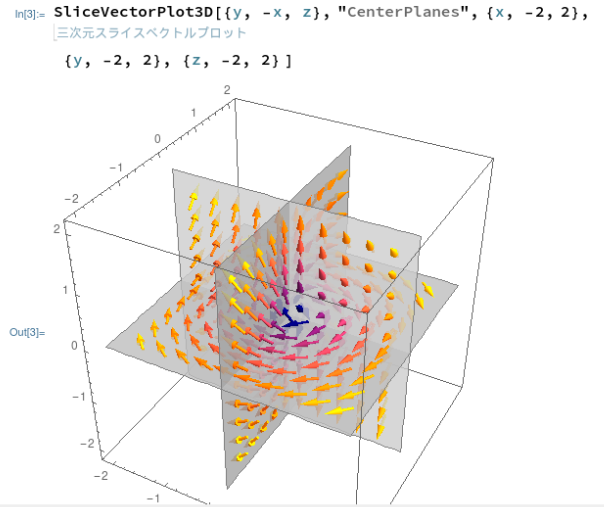
断面毎に描いてくれているので、こちらの方法の方が、ゴチャゴチャしないで分かり易い気がします。
そしてマウスでドラッグすれば、回転させて別な方向から眺めることも可能です。こんな感じ。
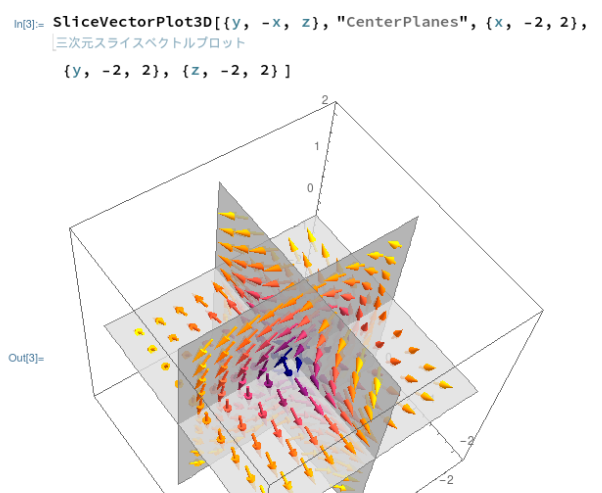
しかし、残念なことに手元のラズパイ３機では、回転のために１回ドラッグすると「分」で時間がかかるので、グリグリと回転させるのは望み薄であります。表示はカッコいいんだけどな～。ラズパイ４にMathematicaインストールしたいなあ。