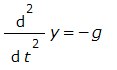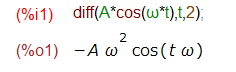いよいよというか、ようやくというかMathematicaとMaximaの練習が微分方程式にたどり着きました。とは言え、そんな１回やそこらで収まるものとも思えませぬ。易しいところから緩々とやる所存でございます。まずは常微分方程式(ODE)から。物理系でおなじみの「答え」の分かっているものから触ってみます。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版）です。Mathematicaはラズパイ上の12.2.0.0です。
勝手に参照させていただいておりますWolfram社Mathematicaのチュートリアルは以下です。
学生でもないのにすみません。
今回、Maximaについては、以下のページを参照させていただいております。弘前大の方のページです。
やっぱりね、数学というよりかは物理、それもあまりディープでない「日常の感覚」で分かるあたりがうれしいです。
ODEを解析的に解く
Maximaの場合、ラプラス変換ベースで微分方程式を解いているらしい desolve()関数があるのでまずそれを使ってみます（そうでないらしい関数もあるのですが、また今度。）手順は以下のようで良いですかね。
- 微分方程式を定義する
- atvalue()関数で、初期値を定義する
- desolve()関数で解く
上記例では、「振動する波形」が出てくるはず。出てまいりました。良かった。でもチトめんどい。一応、検算いたします。２階微分したら「元にもどり」ました。
Mathematicaの場合は、手順逆転、
- 先にDSolveValue[]関数で一般解を求める
- 後から積分定数をテキトーに与える
さきほどのMaximaが制約条件的なものを先に与えてその中で解いているのと異なり、条件なしに先に一般解求めているので、結果が違いますわな。Cosだけでなく、Sinも残ってしまうからかね。
積分定数に無理やり値 A を与えているのが「C[1] -> A」、それを 「/. で一般解sol」の中に全て適用、という記法のようです。
ODEを数値的に解く
Maximaの場合、ルンゲクッタ法を行う関数 rk()があるので、これに常微分方程式を渡して数値的に解くことが可能みたいです。ただし、rk()は２階の方程式をうけつけないので、高階なときは、「１階の方程式までバラシて」「連立させて」与える必用があるみたいです。冒頭のアイキャッチ画像に掲げたような「地球へ向かってのリンゴの落下」みたいな２階の式は、１本でなく、以下のように２本にわけて与えてみます。位置yを時間微分したら速度v、速度を時間微分したら加速度g（yを上向きにとると-g. 当然の9.8m毎秒毎秒)
F1(y, v, t) := v F2(y, v, t, g):= -g t0: 0; t1: 2; N: 100; h: float((t1-t0)/N); data0: rk([F1(y, v, t), F2(y, v, t, 9.8)],[y,v],[0,0],[t, t0, t1, h])$ ylis: makelist([c[1],c[2]], c, data0)$ vlis: makelist([c[1],c[3]], c, data0)$
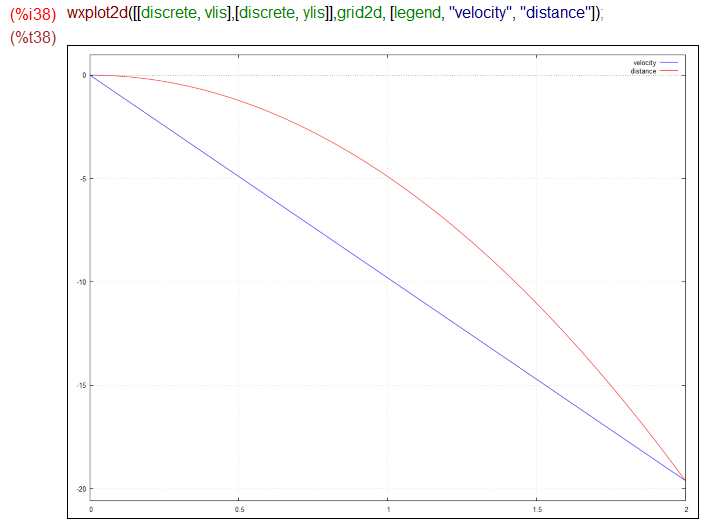
上記のようなステップでルンゲクッタ法で数値的に解をもとめた後で、以下のようにグラフを描くことができました。ただし解には、tとyとvの３組の系列が並んでいるのでグラフにするまえにtとy, tとvの２組に要分離です。リンゴ「落ちて」ますな。わざわざルンゲクッタ法を適用する必要もない方程式だけれども。確かめるのはこれが一番簡単。
一方、Mathematicaの場合、２階であろうと、そのまま数値解を求めるNDSolve[]関数に渡せるようです。解いてみたところが以下に。x[0]==1のところは、そうしないと上手く結果が出なかったため（0にしたらエラーでました。何か前の操作が残っていた？）なぜに1m上から落とすのが良いのか不明。素人には良く分からぬ挙動。
結果のプロットは以下で。再びの /. 登場。この辺の演算子みたいなものも勉強しないとよくわかりまへん。
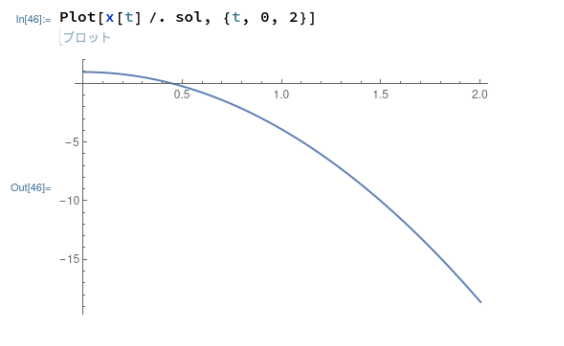
でも、こちらも「落ちて」ますな。「それでも地球は回っている」はガリレオか、違うな。出来ることより、良く分からないことの方が多いので、グズグズといろいろ解いて慣れるしかない？凡人は。